振動子の運動方程式 SciPy

振動子の運動方程式

物理に関連する問題として、振動子の運動方程式を解いてみましょう。

例として、単振動子の運動を考えます。

単振動子は、バネにつながれた質点が減衰力や外力を受けずに振動するシンプルなモデルです。

振動子の運動方程式は、次のように表されます。

$$
[
m \frac{d^2x}{dt^2} + c \frac{dx}{dt} + kx = 0
]
$$

ここで、$ (m) $は質量、$ (c) $は減衰係数、$ (k) $はバネ定数です。

これをSciPyを使って数値的に解いて、結果をグラフ化してみましょう。

以下は、質量$ (m = 1) $、減衰係数$ (c = 0.1) $、バネ定数$ (k = 1) $の単振動子の運動方程式を解く例です。

import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt

# 運動方程式を定義
def harmonic_oscillator(x, t, m, c, k):
    dxdt = x[1]  # 速度を表す状態変数
    dvdt = -(c/m) * x[1] - (k/m) * x[0]  # 加速度を表す状態変数
    return [dxdt, dvdt]

# 初期条件とパラメータ
x0 = [1.0, 0.0]  # 初期位置と初速度
m = 1.0          # 質量
c = 0.1          # 減衰係数
k = 1.0          # バネ定数

# 時間の範囲
t = np.linspace(0, 20, 1000)

# 運動方程式を解く
solution = odeint(harmonic_oscillator, x0, t, args=(m, c, k))

# 位置と速度の時間変化をプロット
plt.figure(figsize=(8, 6))
plt.plot(t, solution[:, 0], label='Position')
plt.plot(t, solution[:, 1], label='Velocity')
plt.xlabel('Time')
plt.ylabel('Value')
plt.title('Harmonic Oscillator Motion')
plt.legend()
plt.grid(True)
plt.show()

このコードでは、Scipyの odeint を使用して単振動子の運動方程式を数値的に解いています。

結果は時間と共に変化する位置と速度の変化をグラフ化しています。

位置と速度のグラフが振動する様子が見られます。

[実行結果]

ソースコード解説

このコードは、単振動子（harmonic oscillator）の運動方程式を解いて、その結果をグラフ化するものです。

以下にソースコードの各部分を説明します。

1. モジュールのインポート:

import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt

• numpy は数値計算用ライブラリで、数値配列を処理するために使われます。
• scipy.integrate の odeint は常微分方程式を数値的に解くための関数です。
• matplotlib.pyplot はグラフ描画ライブラリで、データを可視化するために使用されます。

2. 運動方程式の定義:

def harmonic_oscillator(x, t, m, c, k):
   dxdt = x[1]  # 速度を表す状態変数
   dvdt = -(c/m) * x[1] - (k/m) * x[0]  # 加速度を表す状態変数
   return [dxdt, dvdt]

• harmonic_oscillator 関数は、単振動子の運動方程式を定義しています。
• 位置$ (x) $と時間$ (t) $を引数として受け取り、速度$ (dx/dt) $と加速度$ (d^2x/dt^2) $を計算して返します。

3. 初期条件とパラメータの設定:

x0 = [1.0, 0.0]  # 初期位置と初速度
m = 1.0          # 質量
c = 0.1          # 減衰係数
k = 1.0          # バネ定数

• 初期位置と初速度、質量、減衰係数、バネ定数を設定します。

4. 時間の設定:

t = np.linspace(0, 20, 1000)

• np.linspace を使って、$0$から$20$までの範囲を$1000$個の等間隔な点に区切り、時間の配列を作成します。

5. 運動方程式の解を計算:

solution = odeint(harmonic_oscillator, x0, t, args=(m, c, k))

• odeint 関数を使用して、運動方程式を数値的に解きます。
• harmonic_oscillator 関数に初期条件とパラメータを渡し、時間 t の範囲での解を求めます。

6. 位置と速度の時間変化をプロット:

plt.figure(figsize=(8, 6))
plt.plot(t, solution[:, 0], label='Position')
plt.plot(t, solution[:, 1], label='Velocity')
plt.xlabel('Time')
plt.ylabel('Value')
plt.title('Harmonic Oscillator Motion')
plt.legend()
plt.grid(True)
plt.show()

• matplotlib を使用して、時間に対する位置と速度の変化を折れ線グラフでプロットします。
• solution[:, 0] は位置、solution[:, 1] は速度の結果を表します。
• グラフには軸ラベル、タイトル、凡例、グリッド線が追加されます。
• 最後に plt.show() でグラフを表示します。

グラフ解説

[実行結果]

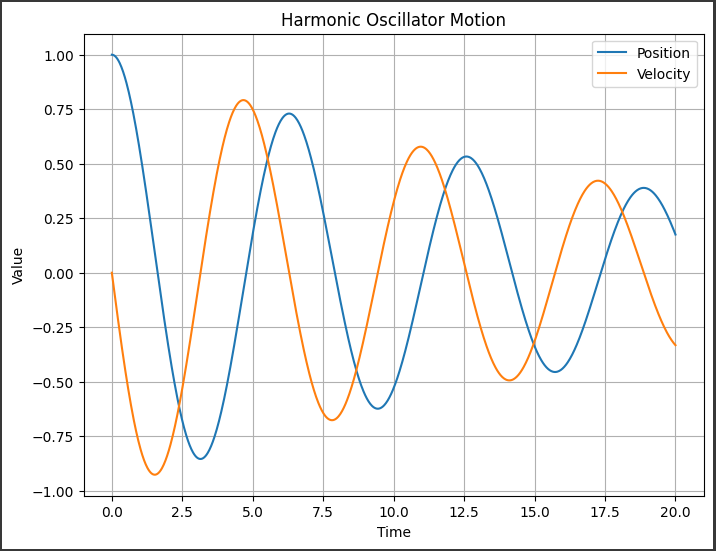
このグラフは、単振動子の振動を時間と共に表現したものです。

1. 位置（Position）のグラフ:

• 横軸は時間を表し、縦軸は単振動子の位置を示しています。
• グラフは、時間の経過とともに振動子の位置が変化する様子を示しています。
  振動子は、特定の周期で正弦波のような動きをします。
  このグラフはその振動の様子を可視化しています。

2. 速度（Velocity）のグラフ:

• 横軸は時間を表し、縦軸は単振動子の速度を示しています。
• 速度グラフは、時間と共に速度がどのように変化するかを示しています。
  振動子は、位置が最大または最小になるときに速度が0になり、その間に速度が最大になることが一般的です。
  このグラフはその速度の変化を示しています。

これらのグラフから、単振動子が周期的に位置と速度が変化する様子を観察できます。

位置と速度の変化が互いに90度ずれた位相で起こり、振動が継続していることがわかります。