最適化問題 PuLP

最適化問題

PuLPを使用して最適化問題を解いてみましょう。

例として、複数の製品を生産する工場があり、利益を最大化するためにそれぞれの製品の生産量を決定したいとします。

以下は、3つの製品 (A, B, C) の生産にかかる時間と利益、および生産できる最大数量の制約条件を考慮した最適化問題です。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
from pulp import LpMaximize, LpProblem, LpVariable

# 問題の定義
model = LpProblem(name="product_production", sense=LpMaximize)

# 変数の定義
prod_A = LpVariable(name="product_A", lowBound=0, cat="Integer")
prod_B = LpVariable(name="product_B", lowBound=0, cat="Integer")
prod_C = LpVariable(name="product_C", lowBound=0, cat="Integer")

# 利益と制約条件の設定
model += 300 * prod_A + 200 * prod_B + 500 * prod_C, "total_profit"

model += 2 * prod_A + 3 * prod_B + 4 * prod_C <= 100  # 生産時間の制約
model += prod_A + prod_B <= 40  # 製品Aと製品Bの同時生産の制約

# 問題の解決
model.solve()

# 結果の出力
print(f"Product A: {prod_A.varValue}")
print(f"Product B: {prod_B.varValue}")
print(f"Product C: {prod_C.varValue}")
print(f"Total Profit: {model.objective.value()}")

# グラフ化
import matplotlib.pyplot as plt

products = ['Product A', 'Product B', 'Product C']
production_quantities = [prod_A.varValue, prod_B.varValue, prod_C.varValue]

plt.figure(figsize=(8, 5))
plt.bar(products, production_quantities, color='skyblue')
plt.xlabel('Products')
plt.ylabel('Production Quantity')
plt.title('Optimal Production Quantities')
plt.show()

このコードを実行すると、最適な製品の生産量とその利益が表示され、それらを棒グラフで可視化することができます。

このように、PuLPを使用して最適化問題を解き、結果を分かりやすくグラフ化することができます。

[実行結果]

ソースコード解説

このコードは、PuLPとMatplotlibを使用して製品生産最適化問題を解き、結果をグラフ化するものです。

1. PuLPの利用

  • from pulp import LpMaximize, LpProblem, LpVariable:
    PuLPの必要なクラスや関数をインポートしています。
  • model = LpProblem(name="product_production", sense=LpMaximize):
    問題を定義するための空のモデルを作成しています。
    ここでは、最大化問題（LpMaximize）としてproduct_productionという名前の問題を作成しています。

2. 変数の定義

  • prod_A, prod_B, prod_C:
    製品A、B、Cのそれぞれの生産量を表す変数を定義しています。
    LpVariableを使用して整数として設定し、0以上の値を取るように制約を設けています。

3. 利益と制約条件の設定

  • model += 300 * prod_A + 200 * prod_B + 500 * prod_C, "total_profit":

目的関数を定義しています。
製品ごとの利益を考慮して、それらの生産量の総利益を最大化するように設定しています。

  • model += 2 * prod_A + 3 * prod_B + 4 * prod_C <= 100:
    生産時間の制約条件を設定しています。
    各製品の生産にかかる時間が合計で100以下であることを意味します。
  • model += prod_A + prod_B <= 40:
    製品AとBの同時生産量に関する制約条件を設定しています。
    製品AとBの合計生産量が40以下であることを要求しています。

4. 問題の解決

  • model.solve():
    定義された最適化問題を解きます。

5. 結果の出力とグラフ化

  • 最適解から得られた製品ごとの生産量と総利益を出力しています。
  • matplotlibを使用して、製品ごとの最適生産量を棒グラフとして可視化しています。

これにより、PuLPを使って製品生産の最適化問題を定義し、解決し、その結果をグラフ化するプロセスが示されています。

結果解説

この問題の解は以下のようになりました：

[実行結果]

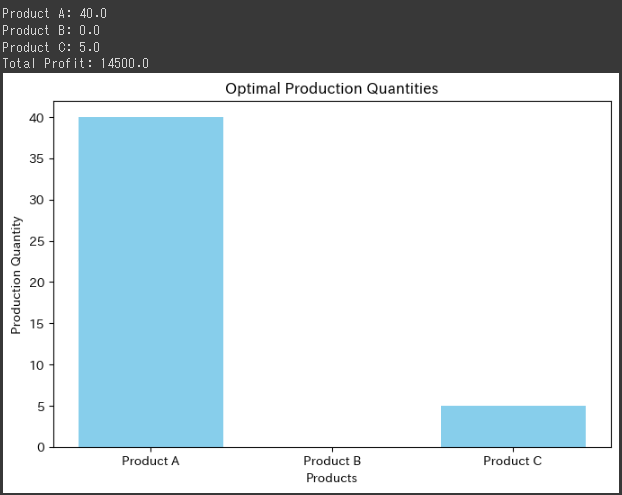
  • 製品Aを40個生産し、製品Bは0個、製品Cは5個生産されます。
  • これにより、総利益は14500になります。

グラフでは、製品ごとの生産量が棒グラフとして示されています。

製品Aが最大生産量である40で、製品Bは制約条件により生産されず、製品Cは5個生産されています。

この生産量のもとで最大の利益である14500が得られます。

製品Bが生産されない理由は、製品Aと製品Bの同時生産に関する制約条件を考慮したためです。

製品Cは比較的高い利益が得られるため、最適解では少量生産されています。