非線形最適化問題 CVXPY

非線形最適化問題

以下のような非線形最適化問題を考えてみましょう。

例題:

最大化する式: (log(x)+√y)

制約条件:

  1. (x2+y2≤50)
  2. (2x−y≥5)
  3. (x≥1)
  4. (y≥1)

これをCVXPYを使って解き、その後結果をグラフで表現してみましょう。

解答例

下記のソースコードは解答例となります。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
import cvxpy as cp
import numpy as np
import matplotlib.pyplot as plt

# 変数の定義
x = cp.Variable()
y = cp.Variable()

# 最大化する式の定義
objective = cp.Maximize(cp.log(x) + cp.sqrt(y))

# 制約条件の定義
constraints = [
    x**2 + y**2 <= 50,
    2*x - y >= 5,
    x >= 1,
    y >= 1
]

# 最適化問題の定義
problem = cp.Problem(objective, constraints)

# 問題を解く
problem.solve()

# 解を表示
print("Optimal value:", problem.value)
print("Optimal x:", x.value)
print("Optimal y:", y.value)

# グラフで可視化
theta = np.linspace(0, 2*np.pi, 100)
circle_x = np.sqrt(50) * np.cos(theta)
circle_y = np.sqrt(50) * np.sin(theta)

plt.figure(figsize=(8, 6))
plt.plot(circle_x, circle_y, label='Constraint 1: x^2 + y^2 <= 50')
plt.fill_between(circle_x, circle_y, color='gray', alpha=0.2)
plt.plot([1, 15], [2 * x.value - 5, 2 * x.value - 5], label='Constraint 2: 2x - y >= 5')
plt.ylim([0, 10])
plt.xlim([0, 10])
plt.scatter(x.value, y.value, color='red', label='Optimal Point')
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.title('Optimization with Constraints')
plt.grid(True)
plt.show()

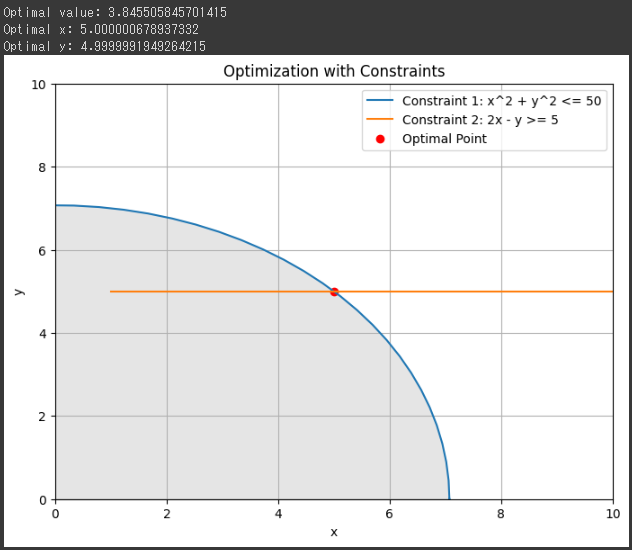
このコードを実行すると、最適な(x)と(y)の値が表示され、また制約条件を含んだグラフも描画されます。

[実行結果]

ソースコード解説

コードの各部分を詳しく見ていきましょう。

1
2
3
import cvxpy as cp
import numpy as np
import matplotlib.pyplot as plt

ここでは、必要なライブラリをインポートしています。

cvxpyは最適化問題を解くためのライブラリで、numpyは数値計算のためのライブラリ、matplotlib.pyplotはグラフ描画のためのライブラリです。

1
2
3
# 変数の定義
x = cp.Variable()
y = cp.Variable()

cp.Variable()を使って最適化問題の変数 x と y を定義しています。

1
2
# 最大化する式の定義
objective = cp.Maximize(cp.log(x) + cp.sqrt(y))

cp.Maximize()を使って最大化したい式を定義しています。

この場合、(log(x)+√y)を最大化します。

1
2
3
4
5
6
7
# 制約条件の定義
constraints = [
    x**2 + y**2 <= 50,
    2*x - y >= 5,
    x >= 1,
    y >= 1
]

constraintsには、最適化問題の制約条件がリストとして定義されています。

ここでは、(x2+y2≤50)、(2x−y≥5)、(x≥1)、(y≥1)という制約条件が設定されています。

1
2
# 最適化問題の定義
problem = cp.Problem(objective, constraints)

cp.Problem()を使って最適化問題を定義しています。

この問題には、先ほど定義した目的関数と制約条件が含まれています。

1
2
# 問題を解く
problem.solve()

problem.solve()を使って定義した最適化問題を解きます。

これにより、最適な解が計算されます。

1
2
3
4
# 解を表示
print("Optimal value:", problem.value)
print("Optimal x:", x.value)
print("Optimal y:", y.value)

ここでは、求められた最適な解の目的関数の値、および(x)と(y)の値を表示しています。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
# グラフで可視化
theta = np.linspace(0, 2*np.pi, 100)
circle_x = np.sqrt(50) * np.cos(theta)
circle_y = np.sqrt(50) * np.sin(theta)

plt.figure(figsize=(8, 6))
plt.plot(circle_x, circle_y, label='Constraint 1: x^2 + y^2 <= 50')
plt.fill_between(circle_x, circle_y, color='gray', alpha=0.2)
plt.plot([1, 15], [2 * x.value - 5, 2 * x.value - 5], label='Constraint 2: 2x - y >= 5')
plt.ylim([0, 10])
plt.xlim([0, 10])
plt.scatter(x.value, y.value, color='red', label='Optimal Point')
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.title('Optimization with Constraints')
plt.grid(True)
plt.show()

最後の部分では、解を可視化するためにmatplotlibを使ってグラフを作成しています。

plt.plot()を使って制約条件を表す円と直線をプロットし、plt.scatter()で最適解を赤い点として表示しています。

これにより、最適化問題の定式化から解の計算、そしてグラフでの視覚化までが行われます。

結果解説

最適な解は、目的関数の値が約3.85で、(x)の値は約5.0、(y)の値は約5.0です。

これは与えられた制約条件の下で最大化された目的関数の値とその(x)、(y)の値です。

グラフでは、以下の内容を示しています：

1. 円形の領域:

制約条件(x2+y2≤50)を表しており、この領域内に解が存在することを示しています。

2. 直線:

制約条件(2x−y≥5)を表しています。
最適解はこの直線の上側に位置しています。

3. 赤い点:

最適解が示されており、目的関数を最大化するための(x)と(y)の値です。

この結果から、与えられた非線形最適化問題において、目的関数を最大化する(x)と(y)の値が見つかりました。

制約条件を満たしつつ、最適な解を見つけることができました。