ポートフォリオ最適化（凸最適化） CVXPY

ポートフォリオ最適化（凸最適化）

CVXPYは凸最適化のためのライブラリです。

以下では、例としてポートフォリオ最適化問題を解いてみましょう。

ポートフォリオ最適化は投資資産の配分を決定する問題で、リスクを最小化しつつ期待収益を最大化する配分を見つけます。

まず、例として適当なデータを生成し、それを用いてポートフォリオ最適化を行います。

その後、結果をグラフ化します。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
import cvxpy as cp
import numpy as np
import matplotlib.pyplot as plt

# データ生成
np.random.seed(42)
n = 5  # 資産の数
mean_returns = np.random.randn(n) / 100  # 平均収益率
cov_matrix = np.random.randn(n, n)
cov_matrix = np.dot(cov_matrix.T, cov_matrix) / 100  # 共分散行列

# ポートフォリオ最適化問題の定義
weights = cp.Variable(n)
expected_return = mean_returns.T @ weights
risk = cp.quad_form(weights, cov_matrix)
constraints = [
    cp.sum(weights) == 1,  # 資産の割合の合計は1
    weights >= 0  # 資産の割合は0以上
]
problem = cp.Problem(cp.Maximize(expected_return - 0.5 * risk), constraints)  # 目的関数

# 最適化
result = problem.solve()

# 結果を表示
print("最適化されたポートフォリオの割合:")
print(weights.value)
print("期待収益率:", expected_return.value)
print("リスク:", np.sqrt(risk.value))

# グラフ化
plt.figure(figsize=(8, 6))
plt.bar(range(n), weights.value, tick_label=[f"Asset {i+1}" for i in range(n)])
plt.xlabel('Assets')
plt.ylabel('Portfolio Weights')
plt.title('Optimized Portfolio Allocation')
plt.show()

このコードは、CVXPYを使ってランダムな収益率と共分散行列を生成し、ポートフォリオの最適な資産割合を求めます。

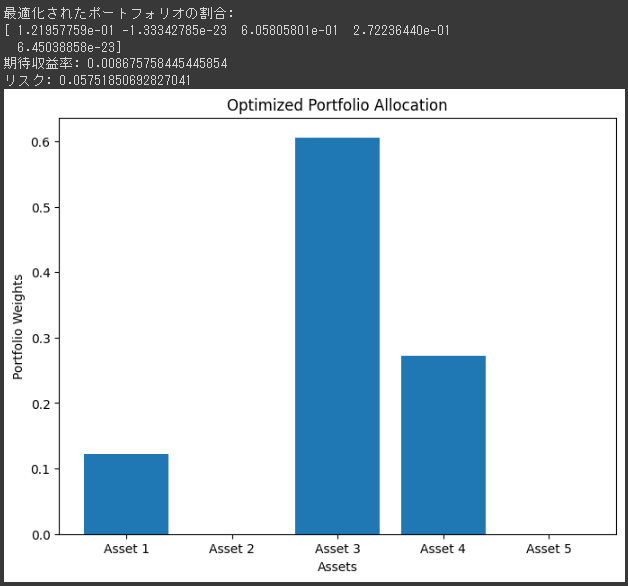
そして、最適化されたポートフォリオの割合を棒グラフで表示します。

[実行結果]

ソースコード解説

以下にソースコードの詳細を示します。

1. ライブラリのインポート

1
2
3
import cvxpy as cp
import numpy as np
import matplotlib.pyplot as plt
  • cvxpyは凸最適化問題を解くためのライブラリです。
  • numpyは数値計算を行うためのライブラリです。
  • matplotlib.pyplotはグラフを描画するためのライブラリです。

2. データの生成

1
2
3
4
5
np.random.seed(42)
n = 5  # 資産の数
mean_returns = np.random.randn(n) / 100  # 平均収益率
cov_matrix = np.random.randn(n, n)
cov_matrix = np.dot(cov_matrix.T, cov_matrix) / 100  # 共分散行列
  • mean_returnsは資産の平均収益率をランダムに生成しています。
  • cov_matrixは共分散行列を生成しています。
    この行列は資産間の関係性（共分散）を表します。

3. ポートフォリオ最適化問題の定義

1
2
3
4
5
6
7
8
weights = cp.Variable(n)
expected_return = mean_returns.T @ weights
risk = cp.quad_form(weights, cov_matrix)
constraints = [
    cp.sum(weights) == 1,  # 資産の割合の合計は1
    weights >= 0  # 資産の割合は0以上
]
problem = cp.Problem(cp.Maximize(expected_return - 0.5 * risk), constraints)  # 目的関数
  • weightsは資産の割合を表す変数です。
  • expected_returnはポートフォリオの期待収益率を表します。
  • riskはポートフォリオのリスクを表します。
  • constraintsでは資産の割合が0以上で合計が1であることを制約として設定しています。
  • problemは最大化する目的関数を定義しています。

4. 最適化

1
result = problem.solve()
  • problem.solve()でポートフォリオ最適化問題を解きます。

5. 結果の表示

1
2
3
4
print("最適化されたポートフォリオの割合:")
print(weights.value)
print("期待収益率:", expected_return.value)
print("リスク:", np.sqrt(risk.value))
  • 最適化されたポートフォリオの割合、期待収益率、リスクを表示しています。

6. グラフ化

1
2
3
4
5
6
plt.figure(figsize=(8, 6))
plt.bar(range(n), weights.value, tick_label=[f"Asset {i+1}" for i in range(n)])
plt.xlabel('Assets')
plt.ylabel('Portfolio Weights')
plt.title('Optimized Portfolio Allocation')
plt.show()
  • 最適化されたポートフォリオの割合を棒グラフで表示しています。
    各資産の割合を視覚的に確認できます。

結果解説

[実行結果]

この結果は、ポートフォリオの最適化後の割合、期待収益率、そしてリスクを示しています。

最適化されたポートフォリオの割合:

各資産の最適な配分を示しています。
例えば、1番目の資産の割合は約12.20%、3番目の資産の割合は約60.58%、4番目の資産の割合は約27.22%となっています。
2番目と最後の資産はほとんど割り当てられていません。

期待収益率:

最適化されたポートフォリオの期待収益率は約0.0087です。
これは、ポートフォリオが1単位投資した場合の平均的なリターンを示しています。

リスク:

ポートフォリオのリスクは、標準偏差またはボラティリティを示しており、約0.0575です。
この値はポートフォリオの変動性を表しています。