広告費用と売上（線形回帰問題） scikit-learn

広告費用と売上（線形回帰問題）

簡単な線形回帰問題を取り上げ、その結果をグラフで可視化します。

問題の設定：

ある小売店が過去の売上データを持っており、広告費用に応じて売上がどのように影響を受けるかを知りたいとします。

具体的には、広告費用と売上の間の関係を線形モデルでモデル化し、広告費用から売上を予測したいと考えます。

以下は、この問題を解決するためのPythonコードの例です：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression

# 仮想的な広告費用と売上データを生成
np.random.seed(0)
X = 10 * np.random.rand(100, 1)
y = 2 * X + 1 + np.random.randn(100, 1)

# 線形回帰モデルの作成と学習
model = LinearRegression()
model.fit(X, y)

# モデルの係数と切片を取得
slope = model.coef_[0]
intercept = model.intercept_

# データと回帰直線のプロット
plt.scatter(X, y, label="Data Points")
plt.plot(X, slope * X + intercept, color='red', label="Regression Line")
plt.xlabel("Advertising Expenses")
plt.ylabel("Sales")
plt.legend()
plt.title("Relationship between Advertising Expenses and Sales")
plt.show()

# 広告費用が10の場合の売上予測
predicted_sales = model.predict([[10]])
print(f"広告費用が10の場合の売上予測: {predicted_sales[0][0]}")

このコードでは、scikit-learnを使用して線形回帰モデルをトレーニングし、広告費用と売上の関係をモデル化しました。

そして、データと回帰直線をグラフで可視化し、広告費用が10の場合の売上を予測しています。

このようにして、scikit-learnを使用して経済的な問題を解決し、その結果をグラフで視覚化することができます。

ソースコード解説

このソースコードは、Pythonを使用して線形回帰を実行し、広告費用と売上の関係をモデル化し、結果を視覚化するプログラムです。

以下はコードの詳細な説明です：

1. ライブラリのインポート:

  • numpyは数値計算用のライブラリで、数学的な演算を効率的に行います。
  • matplotlib.pyplotはグラフを描画するためのライブラリです。
  • sklearn.linear_modelからは線形回帰モデルをインポートします。

2. データ生成:

  • np.random.seed(0)はランダムな値を生成する際のシードを設定して、再現性を確保します。
  • Xは0から10の範囲でランダムに生成された仮想的な広告費用データです。
  • yはXに対応する売上データで、2倍の係数に1を加え、ランダムなノイズを加えて生成されます。

3. 線形回帰モデルの作成と学習:

  • LinearRegression()を使用して線形回帰モデルのインスタンスを作成します。
  • model.fit(X, y)でモデルを訓練します。
    この段階で、広告費用と売上の関係を学習します。

4. モデルの係数と切片を取得:

  • model.coef_はモデルの係数（回帰直線の傾き）を取得します。
  • model.intercept_はモデルの切片（y軸との交点）を取得します。

5. データと回帰直線のプロット:

  • plt.scatter(X, y, label="Data Points")でデータポイントを散布図として描画します。
  • plt.plot(X, slope * X + intercept, color='red', label="Regression Line")で回帰直線を描画します。
    この直線は線形回帰モデルによって最適にフィットされたものです。
  • plt.xlabel("Advertising Expenses")とplt.ylabel("Sales")でX軸とY軸にラベルを追加し、plt.legend()で凡例を表示します。
  • plt.title("Relationship between Advertising Expenses and Sales")でグラフのタイトルを設定します。
  • plt.show()でグラフを表示します。

6. 予測:

  • model.predict([[10]])を使用して、広告費用が10の場合の売上を予測します。
  • print(f"広告費用が10の場合の売上予測: {predicted_sales[0][0]}")で予測結果を表示します。

このコードは、広告費用と売上のデータをもとに線形回帰モデルを構築し、その結果をグラフ化して広告費用と売上の関係を視覚的に理解するのに役立ちます。

また、モデルを使用して新しいデータポイントの売上を予測することも可能です。

グラフ解説

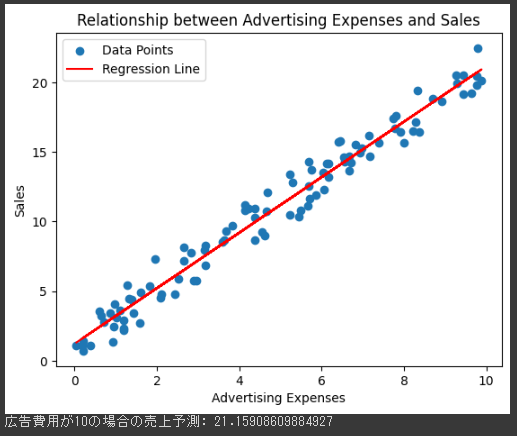
結果と表示されるグラフは「Advertising Expenses（広告費用）」と「Sales（売上）」の関係を示しています。

以下はグラフの詳細な説明です：

- X軸（Horizontal Axis）:

X軸は「Advertising Expenses（広告費用）」を表しており、広告にかけられた費用を示します。
費用は0から10の範囲でランダムに生成されています。

- Y軸（Vertical Axis）:

Y軸は「Sales（売上）」を表しており、各広告費用に対する売上の量を示します。
売上は広告費用に対して線形な関係があると仮定されています。

- 散布図（Scatter Plot）:

グラフ上に散布された点は、実際のデータポイントを表しています。
各点の座標は、広告費用とその広告費用に対応する売上を示しています。

- 回帰直線（Regression Line）:

赤い線が回帰直線を表しています。
この直線は、広告費用と売上の間の線形関係を示しており、線形回帰モデルによって最適にフィットされました。

- ラベル（Labels）:

グラフにはX軸とY軸のラベルが付いており、どの軸が何を表しているかがわかりやすく示されています。

- 凡例（Legend）:

グラフには「Data Points」（データポイント）と「Regression Line」（回帰直線）の2つの要素があり、それぞれの要素が何を表しているかを示す凡例が表示されています。

- グラフタイトル（Graph Title）:

グラフの上部には「Relationship between Advertising Expenses and Sales」（広告費用と売上の関係）というタイトルがあり、グラフの内容を要約しています。

このグラフは、広告費用と売上の間の関係を視覚化し、回帰直線を使用してその関係をモデル化しています。

広告費用が増加するにつれて売上も増加する傾向が見られ、回帰直線がこの関係を表現しています。

このようなグラフを分析することにより、広告費用と売上の間の関係性や予測が可能になります。