最短経路 NetworkX

最短経路

以下の問題を考えてみましょう。

ある都市間の最短経路を見つけるためのネットワークを作成し、最短経路を特定してグラフで表示します。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
import networkx as nx
import matplotlib.pyplot as plt

# 空の有向グラフを作成
G = nx.DiGraph()

# 都市と道路の追加
G.add_node("A", pos=(0, 0))
G.add_node("B", pos=(2, 1))
G.add_node("C", pos=(1, 3))
G.add_node("D", pos=(3, 3))
G.add_node("E", pos=(4, 0))

G.add_edge("A", "B", weight=3)
G.add_edge("A", "C", weight=2)
G.add_edge("B", "C", weight=1)
G.add_edge("B", "D", weight=4)
G.add_edge("C", "D", weight=5)
G.add_edge("C", "E", weight=6)
G.add_edge("D", "E", weight=2)

# ノードの位置を取得
pos = nx.get_node_attributes(G, 'pos')

# グラフを描画
nx.draw(G, pos, with_labels=True, node_size=500, node_color='lightblue', font_size=12, font_color='black')
labels = nx.get_edge_attributes(G, 'weight')
nx.draw_networkx_edge_labels(G, pos, edge_labels=labels)
plt.show()

# 最短経路を計算
shortest_path = nx.shortest_path(G, source="A", target="E", weight="weight")
shortest_path_length = nx.shortest_path_length(G, source="A", target="E", weight="weight")

print("最短経路:", shortest_path)
print("最短距離:", shortest_path_length)

このコードは、都市と道路のネットワークを作成し、最短経路を見つけてグラフで表示します。

結果は最短経路と最短距離が表示されます。

ソースコード解説

ソースコードの詳細な説明を提供します。

1. import networkx as nx および import matplotlib.pyplot as plt:

NetworkXとMatplotlibのライブラリをインポートしています。
これらのライブラリは、グラフの操作と視覚化に使用されます。

2. G = nx.DiGraph():

空の有向グラフ（DiGraph）を作成します。
有向グラフはエッジに向きがあるグラフです。

3. G.add_node("A", pos=(0, 0)) など:

ノード（都市）とその位置情報を追加します。
各都市はラベル（”A”、”B”、”C”など）と2次元座標の位置情報を持っています。

4. G.add_edge("A", "B", weight=3) など:

エッジ（道路）を追加します。
エッジには重み（weight）が設定されており、これは道路の距離やコストを表します。

5. pos = nx.get_node_attributes(G, 'pos'):

ノードの位置情報を取得し、pos に格納します。
後でグラフを描画する際に、ノードを正しい位置に配置するために使用されます。

6. nx.draw(G, pos, with_labels=True, node_size=500, node_color='lightblue', font_size=12, font_color='black'):

グラフを描画します。
ノードは青い円で表示され、ラベルが付けられ、エッジには重みが表示されます。
グラフの見栄えを調整するために、さまざまなパラメータが設定されています。

7. labels = nx.get_edge_attributes(G, 'weight') および nx.draw_networkx_edge_labels(G, pos, edge_labels=labels):

エッジの重み（距離）を取得し、エッジの上に表示します。

8. plt.show():

グラフを表示します。

9. shortest_path = nx.shortest_path(G, source="A", target="E", weight="weight") および shortest_path_length = nx.shortest_path_length(G, source="A", target="E", weight="weight"):

最短経路とその距離を計算します。
ここでは、都市 “A” から都市 “E” への最短経路とその距離を計算しています。

10. print("最短経路:", shortest_path) および print("最短距離:", shortest_path_length):

最短経路とその距離をコンソールに出力します。

このプログラムは、都市間の道路ネットワークを視覚化し、最短経路を計算するための便利なツールとしてNetworkXを使用しています。

結果解説

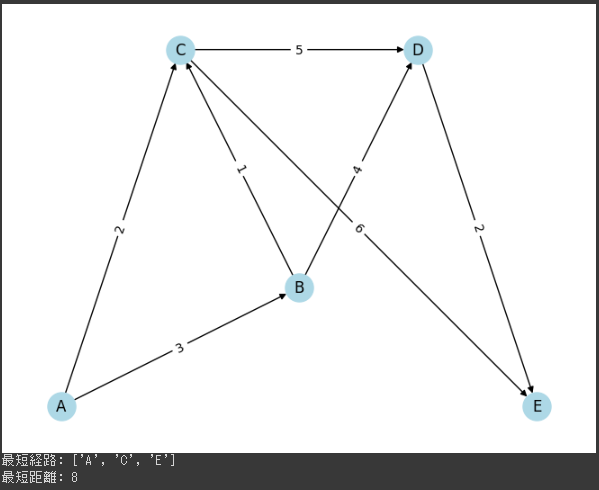
実行結果のグラフは、都市間の道路ネットワークを表しています。

このネットワークを使用して、ある都市から別の都市への最短経路を見つけることができます。

以下に、グラフの詳細な説明を提供します。

1. ノード（Nodes）:

  • ノードは都市を表します。
    このグラフには5つの都市があります。
    それぞれを “A”, “B”, “C”, “D”, “E” とラベル付けています。
  • 各都市の位置は、2次元座標で示されており、グラフを描画する際にそれぞれの位置が考慮されています。

2. エッジ（Edges）:

  • エッジは都市間の道路を表します。
    エッジには重み（weight）が設定されており、それは道路の距離やコストを示しています。
  • 例えば、都市 “A” から都市 “B” への道路の距離は3単位、都市 “B” から都市 “C” への道路の距離は1単位といった具体的な情報がエッジに含まれています。

3. グラフ描画:

  • 上記のコードでは、ノードとエッジの情報をもとに、ネットワークを視覚化しています。
  • ノードは青い円で表され、ノードのラベルが表示されています。
  • エッジには、その重み（道路の距離）が表示されています。

4. 最短経路の計算:

  • コードの最後で、都市 “A” から都市 “E” への最短経路を計算しています。
  • 最短経路は “A” → “C” → “D” → “E” のように表示され、その最短距離は9単位です
    この結果はグラフ上での最短経路を示しています。

このグラフとコードを使用することで、都市間の道路ネットワークにおける最短経路を簡単に計算し、視覚的に表現することができます。