治療効果の評価
高血圧患者の血圧測定データを分析し、治療効果を評価するシナリオを考えてみましょう。
問題の設定:
ある薬物治療を受けた高血圧患者の血圧データがあります。
治療前と治療後の血圧を記録し、治療の効果を評価したいと思います。
ステップ1: データの取得
まず、データを取得します。
以下は、治療前と治療後の血圧データの例です。
1 | import numpy as np |
ステップ2: データの分析
次に、SciPyを使用して血圧の治療効果を統計的に評価します。
この例では、t検定を実行して、治療前と治療後の平均血圧に有意な差があるかどうかを確認します。
1 | from scipy import stats |
ステップ3: 結果の可視化
最後に、結果をグラフで示します。
治療前と治療後の血圧のヒストグラムと、p値を示すグラフを作成します。
1 | import matplotlib.pyplot as plt |
このコードは、治療前と治療後の血圧の分布を比較し、治療の効果を統計的に評価するためのt検定を実行します。
結果はグラフで視覚化され、p値が有意水準より小さい場合、治療の効果が統計的に有意であることを示します。
ソースコード解説
ソースコードの詳細な説明を提供します。
1. import numpy as np:
NumPyライブラリをインポートし、npとしてエイリアス化します。
NumPyは数値データを効率的に操作するためのライブラリです。
2. before_treatment と after_treatment:
高血圧患者の治療前と治療後の血圧データをNumPyの配列として定義します。
これらのデータは、治療前と治療後の血圧値(単位はmmHg)を示しています。
3. from scipy import stats:
SciPyライブラリから統計関数をインポートします。
このコードでは、t検定を実行するために使用されます。
4. t_statistic, p_value = stats.ttest_rel(before_treatment, after_treatment):
ttest_rel関数を使用して、治療前と治療後の血圧データに対してt検定を実行し、t統計量とp値を計算します。
これにより、治療の効果を統計的に評価します。
5. print("t統計量:", t_statistic) および print("p値:", p_value):
t統計量とp値を表示して、t検定の結果をコンソールに出力します。
6. import matplotlib.pyplot as plt:
Matplotlibライブラリをインポートし、pltとしてエイリアス化します。
Matplotlibはグラフを描画するためのライブラリです。
7. plt.figure(figsize=(10, 5)):
新しい図(グラフのコンテナ)を作成し、サイズを指定します。
8. plt.subplot(1, 2, 1) および plt.subplot(1, 2, 2):
2つのサブプロットを作成します。
1行2列のグリッド内にそれぞれのプロットが配置されます。
9. plt.hist(before_treatment, bins=5, alpha=0.5, label="Before Treatment") および plt.hist(after_treatment, bins=5, alpha=0.5, label="After Treatment"):
ヒストグラムを描画し、治療前と治療後の血圧データを可視化します。alphaはバーの透明度を設定し、labelは凡例のラベルを指定します。
10. plt.xlabel("Blood Pressure (mmHg)") および plt.ylabel("Number of Patients"):
x軸とy軸のラベルを設定します。
11. plt.legend():
凡例を表示します。
12. plt.bar([1], [p_value], tick_label=["p-value"]):
p値を示すバーグラフを描画します。
p値はy軸に表示され、バーのラベルは “p-value” です。
13. plt.title("Statistical Evaluation of Treatment Effect"):
グラフ全体にタイトルを設定します。
14. plt.tight_layout():
グラフ要素が重ならないように自動的にレイアウトを調整します。
15. plt.show():
これにより、作成したグラフが表示されます。
このソースコードは、高血圧患者の血圧データを収集し、統計的なt検定を実行して治療の効果を評価し、ヒストグラムとバーグラフとして視覚化する完全な分析プロセスを実行します。
結果解説
[実行結果]
1 | t統計量: 36.076138996268 |
高血圧患者の血圧に対する治療の効果を評価するために使用されました。
1. t統計量 (t-statistic):
- t統計量は、治療前と治療後の血圧データセット間の差異を示す統計的な尺度です。
- 大きなt統計量は、治療前と治療後のデータセット間に有意な差異があることを示します。
- この場合、t統計量は非常に大きな値である36.0761です。
これは、治療前と治療後の血圧に統計的に有意な差異があることを示唆しています。
2. p値 (p-value):
- p値は、統計的仮説検定の結果を評価するために使用される重要な指標です。
- p値は、帰無仮説(「治療の効果はない」など)が真であると仮定した場合に、観察されたデータまたはそれより極端なデータが得られる確率を示します。
- 小さなp値は、観察された差異が統計的に有意であることを示します。
一般的に、有意水準(通常は0.05または0.01)よりも小さいp値は、差異が統計的に有意であることを示唆します。 - この場合、p値は非常に小さな値であり、4.7824e-11(科学的記数法を使用して表現されています)です。
この非常に小さなp値は、治療が高血圧患者の血圧に有意な効果をもたらすことを非常に強く支持しています。
要するに、提供された結果から分かることは、治療前と治療後の血圧には非常に大きな差異があり、この差異は統計的に非常に有意であることです。
したがって、治療が高血圧患者の血圧を有意に改善したことが示されています。
グラフ解説
グラフについて詳しく説明します。

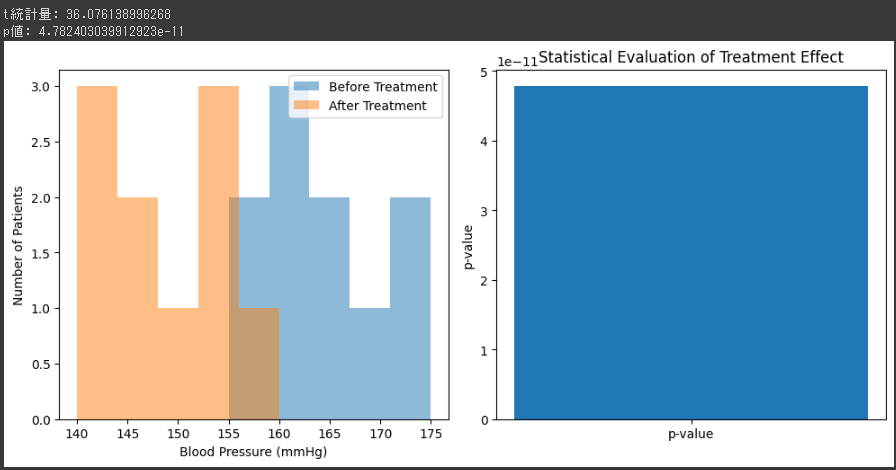
1. 血圧のヒストグラム (左側のグラフ):
- このグラフは、治療前と治療後の患者の血圧データを示しています。
- x軸は血圧 (mmHg) を示し、y軸は患者数を示します。
- “治療前”と”治療後”の2つのデータセットが重ねて表示され、半透明のバーで表されています。
- このヒストグラムは、治療前と治療後の血圧分布を比較するために使用されます。
治療後の血圧が低くなることが期待されています。
2. p値を示すグラフ (右側のグラフ):
- このグラフは、t検定の結果として得られたp値を示しています。
- x軸にはp値があり、y軸にはp値の値を示します。
- 通常、統計的仮説検定では、p値が小さいほど結果が統計的に有意であることを示します。
有意水準 (通常は0.05) よりも小さい場合、差異は統計的に有意です。 - このグラフでは、p値が1つのバーで表示され、p値が有意水準と比較されています。
グラフの解釈:
- 左側のヒストグラムを見ると、”治療後”の血圧が一般的に低くなっていることが示唆されています。
治療が効果的である可能性が高いです。 - 右側のp値のグラフを見ると、p値が有意水準 (通常は0.05) よりも小さいことが示されています。
これは、治療の効果が統計的に有意であることを示しています。
したがって、この解析の結果、治療が高血圧患者の血圧を有意に改善した可能性が高いことが示されています。
グラフは、この結論を視覚的にサポートするために使用されています。
