クロスセル予測 scikit-learn

クロスセル予測

クロスセル予測は、顧客がある商品を購入した後に他の商品を購入する可能性を予測するための手法です。

ここでは、scikit-learnを使用して、顧客がある商品を購入した後に他の商品を購入する可能性を予測する簡単な例を示します。

1.ライブラリのインポート

これらのライブラリは、データの操作、可視化、モデルの訓練と評価に必要です。

1
2
3
4
5
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import confusion_matrix
2.データの生成

ここでは、500人の顧客が商品Aを購入し、そのうち200人が商品Bも購入しているというデータを生成しています。

Xは顧客の特徴量を表し、yは商品Bを購入したかどうかを表します。

1
2
3
4
5
6
7
8
9
10
11
12
# 商品Aを購入した顧客の数
n_customers = 500

# 商品Aを購入した顧客のうち、商品Bも購入した顧客の数
n_cross_sell = 200

# 商品Aを購入した顧客の特徴量（ここではランダムに生成）
X = np.random.rand(n_customers, 10)

# 商品Bを購入したかどうかのラベル（最初のn_cross_sell人は1、残りは0）
y = np.zeros(n_customers)
y[:n_cross_sell] = 1
3.データの分割

データを訓練データとテストデータに分割します。

訓練データはモデルの学習に、テストデータはモデルの性能評価に使用します。

1
2
# データを訓練データとテストデータに分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
4.モデルの訓練

ランダムフォレスト分類器を使用してモデルを訓練します。

ランダムフォレストは、複数の決定木を組み合わせて予測を行うアルゴリズムです。

1
2
3
4
5
# ランダムフォレスト分類器のインスタンスを作成
clf = RandomForestClassifier(n_estimators=100, random_state=42)

# モデルを訓練
clf.fit(X_train, y_train)
5.予測と評価

訓練したモデルを使用してテストデータのクロスセルを予測し、混同行列を計算します。

混同行列は、モデルの性能を評価するための表です。

1
2
3
4
5
# テストデータのクロスセルを予測
y_pred = clf.predict(X_test)

# 混同行列を計算
cm = confusion_matrix(y_test, y_pred)
6.結果の可視化

混同行列をヒートマップとして表示します。

これにより、モデルの性能を視覚的に理解することができます。

1
2
3
4
5
6
7
8
9
10
11
# 混同行列を表示
plt.imshow(cm, interpolation='nearest', cmap=plt.cm.Blues)
plt.title('Confusion matrix')
plt.colorbar()
tick_marks = np.arange(2)
plt.xticks(tick_marks, ['No Cross-sell', 'Cross-sell'], rotation=45)
plt.yticks(tick_marks, ['No Cross-sell', 'Cross-sell'])
plt.tight_layout()
plt.ylabel('True label')
plt.xlabel('Predicted label')
plt.show()
[実行結果]

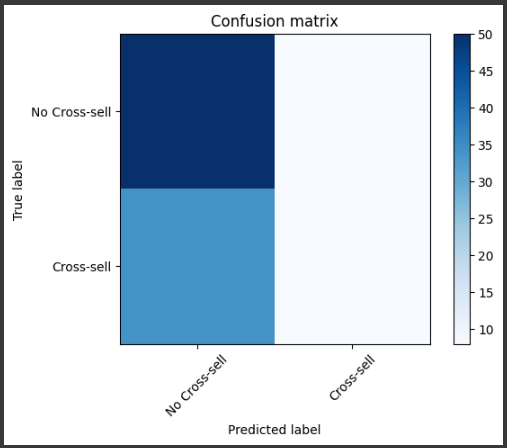
実際の問題では、顧客の特徴量をより詳細に把握するために、購入履歴や顧客のデモグラフィック情報など、さまざまなデータを使用することがあります。

また、モデルの性能を向上させるために、パラメータのチューニングや他の機械学習アルゴリズムの使用もあります。

混同行列（Confusion Matrix）

モデルの予測結果は、混同行列（Confusion Matrix）によって表現されます。

混同行列は、実際のクロスセルのラベルと予測されたクロスセルのラベルを比較し、それらの関係を可視化します。

混同行列は4つのセルで構成されます：

  • 真陽性（True Positive; TP）:
    実際のラベルが「クロスセルあり」であり、予測も「クロスセルあり」の場合。
  • 真陰性（True Negative; TN）:
    実際のラベルが「クロスセルなし」であり、予測も「クロスセルなし」の場合。
  • 偽陽性（False Positive; FP）:
    実際のラベルが「クロスセルなし」であり、予測が「クロスセルあり」となった場合。
  • 偽陰性（False Negative; FN）:
    実際のラベルが「クロスセルあり」であり、予測が「クロスセルなし」となった場合。

混同行列の各セルには、実際のデータポイントの数が表示されます。

モデルが正しく予測した場合は真陽性（TP）や真陰性（TN）の数が高くなり、誤った予測があった場合は偽陽性（FP）や偽陰性（FN）の数が増えます。

この例では、混同行列が表示されると、x軸が予測ラベル、y軸が実際のラベルであり、それぞれのセルに該当するデータポイントの数が表示されます。

これにより、モデルの予測結果の正確さやエラーの傾向を評価することができます。

また、混同行列から算出される指標として、精度（Accuracy）、再現率（Recall）、適合率（Precision）、F1スコア（F1 Score）などがあります。

これらの指標は、モデルの性能評価や比較に使用されます。