最小二乗ベクターマシン CVXPY

最小二乗ベクターマシン

最小二乗ベクターマシン（Least Squares Support Vector Machine, LS-SVM）は、サポートベクターマシン（SVM）の一種で、最小二乗法を用いて分類問題や回帰問題を解く手法です。

ここでは、2次元の線形分類問題を例に、CVXPYを使ってLS-SVMを実装してみましょう。

まず、サンプルデータを生成します。

2つのクラスが線形に分離可能なデータセットを作成します。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
import numpy as np
import matplotlib.pyplot as plt

np.random.seed(0)

# クラス1のデータ生成
mean1 = np.array([0, 2])
cov1 = np.array([[1, 0.8], [0.8, 1]])
class1_data = np.random.multivariate_normal(mean1, cov1, 50)

# クラス2のデータ生成
mean2 = np.array([2, 0])
cov2 = np.array([[1, 0.8], [0.8, 1]])
class2_data = np.random.multivariate_normal(mean2, cov2, 50)

# データのプロット
plt.scatter(class1_data[:, 0], class1_data[:, 1], label='Class 1')
plt.scatter(class2_data[:, 0], class2_data[:, 1], label='Class 2')
plt.legend()
plt.show()
[実行結果]

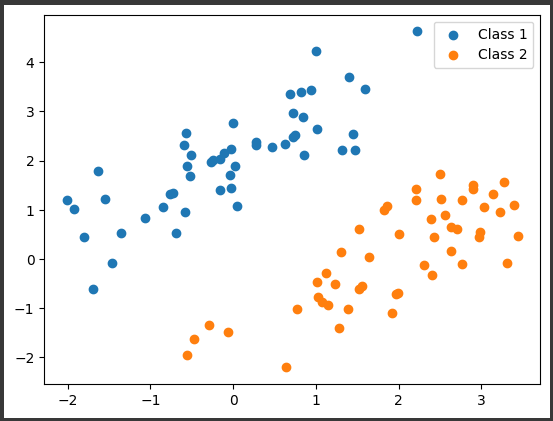
次に、CVXPYを使ってLS-SVMを実装します。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
import cvxpy as cp

# データの準備
X = np.vstack((class1_data, class2_data))
y = np.hstack((np.ones(50), -np.ones(50)))

# 変数の定義
w = cp.Variable(2)
b = cp.Variable()
xi = cp.Variable(100)

# パラメータの設定
C = 1

# 目的関数の定義
objective = cp.Minimize(cp.sum_squares(w) / 2 + C * cp.sum(xi))

# 制約条件の定義
constraints = [cp.multiply(y, (X @ w + b)) >= 1 - xi, xi >= 0]

# 最適化問題の定義と解決
prob = cp.Problem(objective, constraints)
prob.solve()

# 最適解の取得
w_opt = w.value
b_opt = b.value

print("Optimal w:", w_opt)
print("Optimal b:", b_opt)
[実行結果]

最後に、分類境界線をプロットします。

1
2
3
4
5
6
7
8
9
# 分類境界線のプロット
x_line = np.linspace(-2, 4, 100)
y_line = -(w_opt[0] * x_line + b_opt) / w_opt[1]

plt.scatter(class1_data[:, 0], class1_data[:, 1], label='Class 1')
plt.scatter(class2_data[:, 0], class2_data[:, 1], label='Class 2')
plt.plot(x_line, y_line, color='red', label='Decision boundary')
plt.legend()
plt.show()
[実行結果]

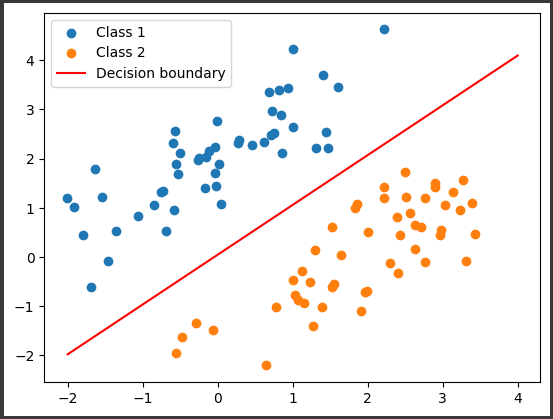
このコードは、2次元の線形分類問題に対してLS-SVMを適用し、最適な分類境界線を求めるものです。

CVXPYを使って最適化問題を定義し、最適解を求めています。