NetworkX⑥（最短経路問題）

最短経路問題

複数の経路の中から、最も効率の良い経路 を求める問題を 最短経路問題 といいます。

「効率のよい」という意味としては、「時間が短い、費用が安い、距離が短い」などさまざまな基準があります。

NetworkX では、このような基準を weight として数値化します。

まず、最短経路を求めるグラフを定義し、図示してみます。

[Google Colaboratory]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
import networkx as nx

G = nx.DiGraph()

# 始点ノード、終了ノード、重さ(weight)を定義
G.add_weighted_edges_from(
    [('A', 'B', 4), ('A', 'C', 3), ('B', 'C', 1), ('B', 'D', 1), ('B', 'E', 5), 
     ('C', 'F', 2), ('D', 'E', 3), ('F', 'E', 1), ('E', 'G', 2), ('F', 'G', 4), ]
)

# ノードの位置（グラフ描画用） => ノード名:(横位置, 縦位置)
pos = {'A': (0, 1), 'B': (1, 2), 'C': (1, 0), 'D': (2, 1), 'E': (3, 2),
       'F': (3, 0), 'G': (4, 1)}

edge_labels = {}
for (i, j) in G.edges():
    edge_labels[i, j] = f"{ G[i][j]['weight'] }"

nx.draw(G, pos=pos, with_labels=True, node_size=500)
nx.draw_networkx_edge_labels(G, pos, edge_labels=edge_labels)

[実行結果]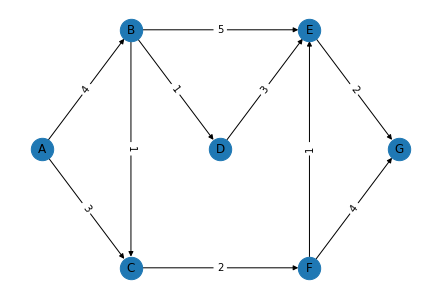

ダイクストラ法

最短経路問題 を解くためには、NetworkX の dijkstra_path_length関数 を使います。

[Google Colaboratory]

1
2
3
4
5
6
7
8
# ダイクストラ法で最短経路とその重み（最小コスト）を求める
start, end = "A", "G"
shortest_path = nx.dijkstra_path(G, start, end)
shortest_path_weight = nx.dijkstra_path_length(G, start, end)

# 出力
print("Shortest Path:", shortest_path)
print("Weight:", shortest_path_weight)

[実行結果]

Shortest Path: ['A', 'C', 'F', 'E', 'G']
Weight: 8

最短経路は ‘A’ ➡ ‘C’ ➡ ‘F’ ➡ ‘E’ ➡ ‘G’ となり、最小コスト（トータルの重さ）は 8 であることを導き出すことができました。