NetworkX⑤（最小カット問題）

NetworkXを、使って 最小カット問題 を解いてみます。

最小カット問題

グラフに対してｓからｔへのパスが存在しなくなるために除去しなければいけない辺の 容量の和の最小値 を求める問題を 最小カット問題 といいます。

前回記事で使ったグラフをもう一度作成します。

[Google Colaboratory]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
import networkx as nx

G = nx.DiGraph()

#(始点，終点，重み)でエッジを設定
G.add_edges_from([('s', '1', dict(capacity=10)),
                  ('s', '2', dict(capacity=2)),
                  ('1', '2', dict(capacity=6)),
                  ('1', '3', dict(capacity=6)),
                  ('3', '2', dict(capacity=3)),
                  ('2', 't', dict(capacity=5)),
                  ('3', 't', dict(capacity=8)),
])

#エッジラベルの描画時に'capacity'の表示を無くすための工夫
edge_labels = {(i, j): w['capacity'] for i, j, w in G.edges(data=True)}
pos = nx.spring_layout(G, k=10)
nx.draw_networkx_edge_labels(G,pos, edge_labels=edge_labels)

# グラフの描画
nx.draw_networkx(G, pos)

[実行結果]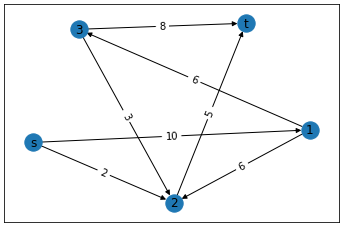

解法

最小カット問題 を解くためには、minimum_cut関数 を使います。

引数には、グラフオブジェクト、始点ノード、終了ノード を設定します。

[Google Colaboratory]

1
2
3
4
5
cut_value, partition = nx.minimum_cut(G, 's', 't')
print(f'cut value: {cut_value}')

S, T = partition
print(f'  (S, T): ({S}, {T})')

[実行結果]

cut value: 11

  (S, T): ({'1', '2', 's'}, {'3', 't'})

始点側のノードの集合は {‘1’, ‘2’, ‘s’} で、終点側の集合は {‘3’, ‘t’} となりました。

この集合２つをつなぐエッジ（辺）の容量の和は 11 であり、これが最小となります。

最小カット問題 の解は 最大流問題 と解は同じとなり、最大流最小カット定理 と呼ばれます。