ロジスティック回帰モデル① （構築）

ロジスティック回帰は、二値分類でよく使われる手法で、回帰分析のプロセスを経て分類予測を行います。

ロジスティック回帰では、重み付けされた説明変数の和から、一方に分類される確率を算出し閾値（50%）を上回るかどうかで最終的な分類を決定します。

良性に分類される確率が40%であれば悪性に分類されることになります。

ロジスティック回帰モデルの構築

ロジスティック回帰モデルを構築するには、scikit-learnのLogisticRegressionクラスを使用します。

[Google Colaboratory]

1
2
3
from sklearn.linear_model import LogisticRegression

log_reg = LogisticRegression(random_state=0).fit(X_train_scaled, y_train)

予測結果を出力します。

[Google Colaboratory]

1
2
3
4
5
y_train_pred = log_reg.predict(X_train_scaled)
y_test_pred = log_reg.predict(X_test_scaled)

print(y_train_pred[:5])
print(y_test_pred[:5])

[実行結果]

ラベルデータである0, 1がきちんと出力されていることが分かります。

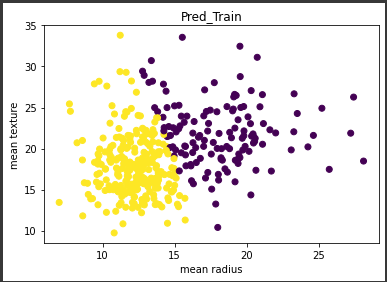
可視化（訓練データ）

訓練データの予測結果を可視化します。

[Google Colaboratory]

1
2
3
4
5
plt.scatter(X_train["mean radius"],X_train["mean texture"], c=y_train_pred)
plt.title("Pred_Train") 
plt.xlabel("mean radius")
plt.ylabel("mean texture")
plt.show()

[実行結果]

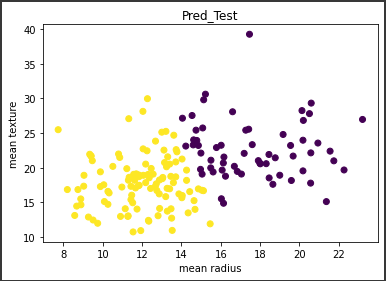
可視化（テストデータ）

テストデータの予測結果を可視化します。

[Google Colaboratory]

1
2
3
4
5
plt.scatter(X_test["mean radius"],X_test["mean texture"], c=y_test_pred)
plt.title("Pred_Test") 
plt.xlabel("mean radius")
plt.ylabel("mean texture")
plt.show()

[実行結果]

ある直線を境にきれいにデータが２分割されています。

次回は、この直線に焦点を当てて可視化を行います。