PCAとUMAPの組み合わせ(次元削減)

高次元データを扱う場合、UMAPのみで次元削減するのではなくPCAの結果をさらにUMAPで次元削減することでよりよい結果になることがあります。

PCA実行

前回と同様にMNISTのデータセットを使って、PCAで次元削減してみます。

[Google Colaboratory]

1
2
3
4
5
6
pca = PCA(n_components=0.99, random_state=0)
X_pc = pca.fit_transform(digits.data)
df_pca = pd.DataFrame(X_pc, columns=["PC{}".format(i + 1) for i in range(len(X_pc[0]))])
print("主成分の数: ", pca.n_components_) 
print("保たれている情報: ", np.sum(pca.explained_variance_ratio_))
display(df_pca.head())

[実行結果(一部略)]

n_componentsに0.99を指定している（1行目）ので、累積寄与率が99%になるPC41までが結果として表示されました。

もともとは64次元でしたので23次元が削減されたことになります。

UMAPとPCA+UMAPの比較

PCAの結果に対してさらにUMAPを実行します。(2行目)

また比較のためにUMAPのみを実行した場合の結果も合わせて表示します。(1行目)

n_neighborsには5, 10, 15を指定します。

[Google Colaboratory]

1
2
create_2d_umap(digits.data, digits.target, digits.target_names, [5,10,15])
create_2d_umap(df_pca, digits.target, digits.target_names, [5,10,15])

[実行結果]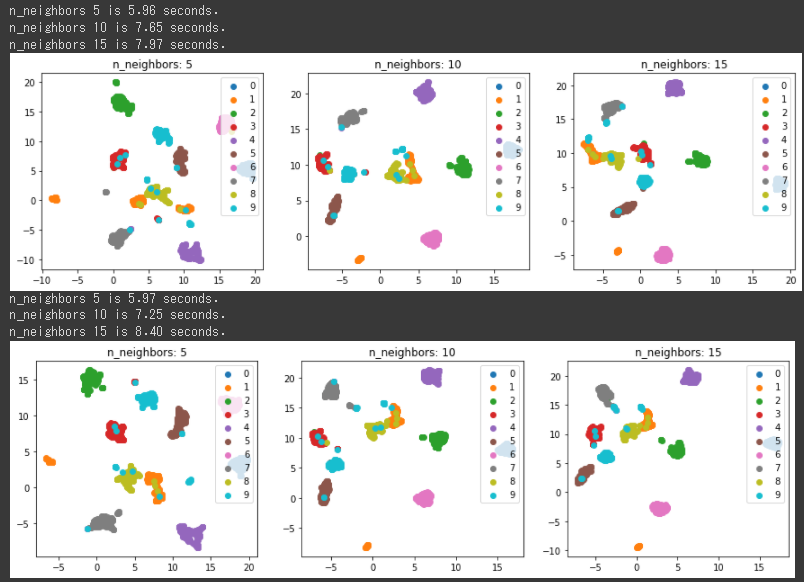

上図がUMAPのみの結果、下図がPCA+UMAPの結果となります。

明確にどちらの分類がよいか判断が難しいところですが、分類結果が変わっていることは確認できます。

PCAとUMAPを組み合わせた手法があるということも覚えておくと検証の幅が広がるかと思います。