ニューラルネットワークでアヤメ分類

アヤメデータの分類をニューラルネットワークで行います。
まずは必要なモジュールをインポートします。

1
2
3
import numpy as np
import matplotlib.pyplot as plt
import sklearn.datasets as ds

アヤメデータを読み込みます。

1
2
3
4
5
6
# アヤメデータを読み込む
Iris = ds.load_iris()
xdata = Iris.data.astype(np.float32)  # アヤメデータの特徴量
tdata = Iris.target.astype(np.int32)  # アヤメの種類（答え）

D, N = xdata.shape     # D=150, N=4   # 4種類の特徴量が150データ分

読み込んだデータを訓練データとテストデータに分けます。半分ずつにします。

1
2
3
4
5
6
7
# 訓練データとテストデータに分ける
Dtrain = D // 2     # 75
index = np.random.permutation(range(D))  # ランダムなインデックスを作成
xtrain = xdata[index[0:Dtrain],:]  # 訓練データの入力
ttrain = tdata[index[0:Dtrain]]    # 訓練データのラベル（正解）
xtest = xdata[index[Dtrain:D],:]   # テストデータの入力
ttest = tdata[index[Dtrain:D]]     # テストデータのラベル（正解）

Chainerを使えるように宣言します。

1
2
3
4
5
# Chainerの宣言
import chainer.optimizers as Opt
import chainer.functions as F
import chainer.links as L
from chainer import Variable, Chain, config

３層のニューラルネットワークを作成します。

1
2
3
# ３層のニューラルネットワークを作成
C = np.max(tdata) + 1
NN = Chain(l1=L.Linear(N, 3), l2=L.Linear(3, 3), l3=L.Linear(3, C))

３層ニューラルネットワークを関数化します。

①ニューラルネットワークの関数化
1
2
3
4
5
6
7
8
# ３層ニューラルネットワークの関数化
def model(x):
    h = NN.l1(x)
    h = F.sigmoid(h)
    h = NN.l2(h)
    h = F.sigmoid(h)
    y = NN.l3(h)
    return y

最適化手法を設定します。

②最適化手法を設定
1
2
3
# 最適化手法を設定
optNN = Opt.SGD()
optNN.setup(NN)

学習結果を記録する変数を定義します。

1
2
3
4
5
# 学習の記録用
train_loss = []
train_acc = []
test_loss = []
test_acc = []

学習処理を実装します。学習回数は1000回です。

③学習処理
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
T = 1000
for time in range(T):
    config.train = True
    optNN.target.zerograds()
    ytrain = model(xtrain)
    loss_train = F.softmax_cross_entropy(ytrain, ttrain)
    acc_train = F.accuracy(ytrain, ttrain)
    loss_train.backward()
    optNN.update()
    
    config.train = False
    ytest = model(xtest)
    loss_test = F.softmax_cross_entropy(ytest, ttest)
    acc_test = F.accuracy(ytest, ttest)

    train_loss.append(loss_train.data)
    train_acc.append(acc_train.data)
    test_loss.append(loss_test.data)
    test_acc.append(acc_test.data)

結果の誤差をグラフ表示します。

④誤差のグラフ表示
1
2
3
4
5
6
7
8
9
10
11
12
# 学習記録の表示(誤差)
Tall = len(train_loss)
plt.figure(figsize=(8, 6))
plt.plot(range(Tall), train_loss, label='train_loss')
plt.plot(range(Tall), test_loss, label='test_loss')
plt.title('loss function in training and test')
plt.xlabel('step')
plt.ylabel('loss function')
plt.xlim([0, Tall])
plt.ylim(0, 4)
plt.legend()
plt.show()

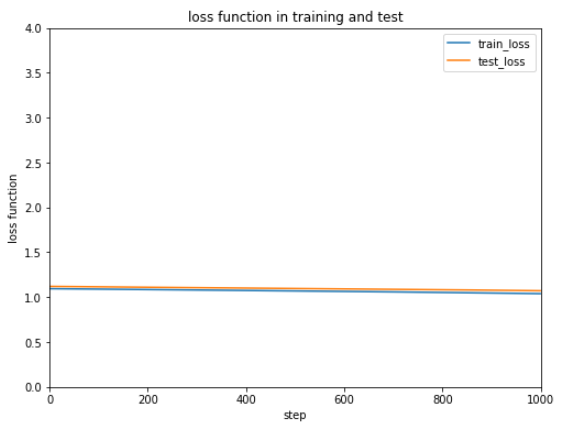誤差
ほとんど変わっていないようにみえます。
正解率もグラフ化します。

⑤正解率のグラフ表示
1
2
3
4
5
6
7
8
9
10
11
# 学習記録の表示(正解率)
plt.figure(figsize=(8, 6))
plt.plot(range(Tall), train_acc, label='train_acc')
plt.plot(range(Tall), test_acc, label='test_acc')
plt.title('accuracy in training and test')
plt.xlabel('step')
plt.ylabel('accuracy')
plt.xlim([0, Tall])
plt.ylim(0, 1.0)
plt.legend()
plt.show()

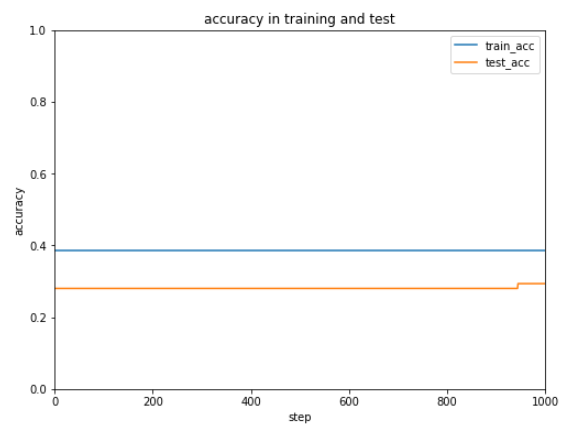正解率
ぜんぜん正解率があがりません。あきらめずにもう10,000回実行してみます。
先ほどの1,000回と合わせてトータルで11,000回実行することになります。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
T = 10000   # 学習回数を10倍に変更
for time in range(T):
    config.train = True
    optNN.target.zerograds()
    ytrain = model(xtrain)
    loss_train = F.softmax_cross_entropy(ytrain, ttrain)
    acc_train = F.accuracy(ytrain, ttrain)
    loss_train.backward()
    optNN.update()
    
    config.train = False
    ytest = model(xtest)
    loss_test = F.softmax_cross_entropy(ytest, ttest)
    acc_test = F.accuracy(ytest, ttest)

    train_loss.append(loss_train.data)
    train_acc.append(acc_train.data)
    test_loss.append(loss_test.data)
    test_acc.append(acc_test.data)

④誤差のグラフ表示と⑤正解率のグラフ表示を再び実行します。
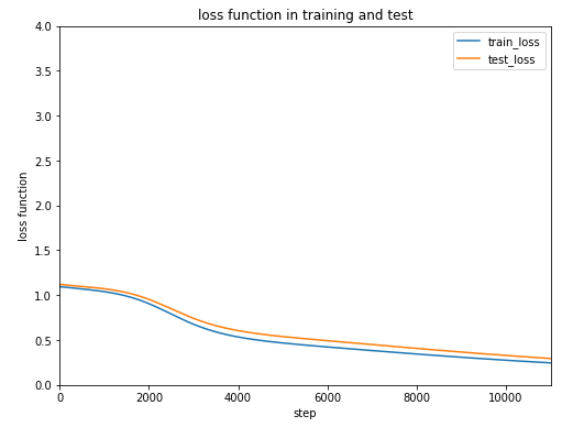誤差
誤差は緩やかながらだんだん減少しているようです。
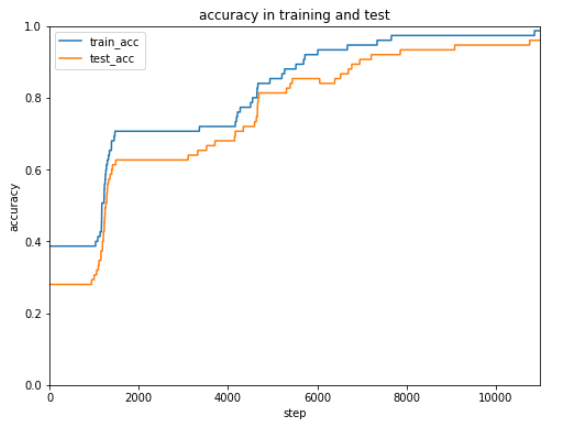正解率
正解率は２段階にわけて正解率がぐんとあがることがあり、最終的にはほぼ100%の正解率になってます。あきらめずに続けるって大切ですね。

しかしもっと効率よく学習する方法があります。
それは非線形変換をシグモイドからReLUに変更することです。複雑なニューラルネットワークを利用するときはReLUの方がよいとのことです。
①ニューラルネットワークの関数化を下記のように変更します。

①ニューラルネットワークの関数化を変更
1
2
3
4
5
6
7
8
# 非線形変換をシグモイドからReLUに変更
def model(x):
    h = NN.l1(x)
    h = F.relu(h)
    h = NN.l2(h)
    h = F.relu(h)
    y = NN.l3(h)
    return y

ニューラルネットワークをもう一度生成し、最適化手法を再設定、学習の記録用データをリセットしたあとに、③学習処理(1,000回)と④誤差のグラフ表示、⑤正解率のグラフ表示を実行してみます。

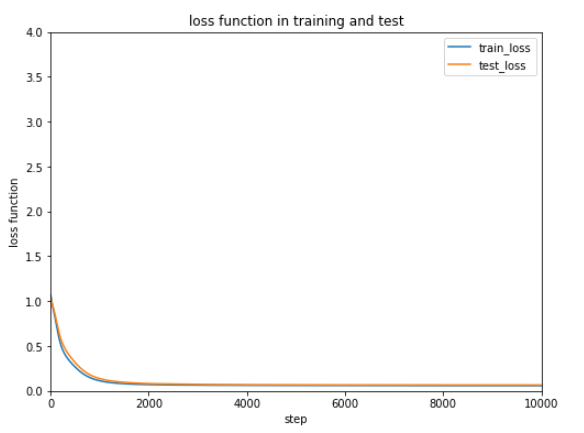誤差

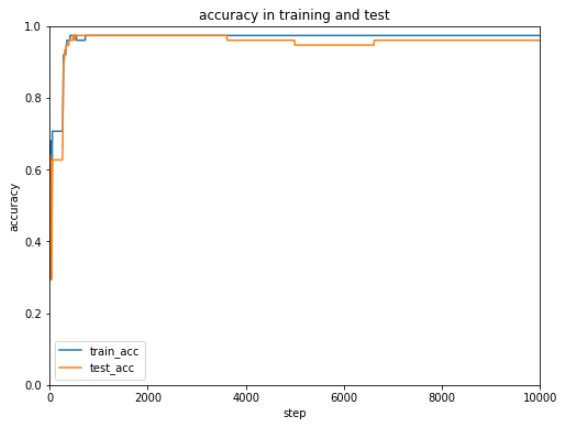正解率
確かにシグモイドよりReLUを使った方が早く誤差、正解率ともに改善していることが分かります。

(Google Colaboratoryで動作確認しています。)