ニューラルネットワークでデータの分類をしてみます。
まずは、chainerの宣言をします。
1
2
3
4
| import chainer.optimizers as Opt
import chainer.functions as F
import chainer.links as L
from chainer import Variable, Chain, config
|
次に乱数を生成します。100行2列のデータとなります。
1
2
3
4
5
6
| import numpy as np
import matplotlib.pyplot as plt
D = 100
N = 2
xdata = np.random.randn(D * N).reshape(D, N).astype(np.float32)
|
次にデータを分割する関数とその関数で分類したデータを準備します。
1
2
3
4
| def f(x):
return x * x
tdata = (xdata[:,1] > f(xdata[:,0])).astype(np.int32)
|
1層のニューラルネットワーク作成します。
2種類のデータが入力され、2種類のデータ出力される単純なニューラルネットワークとなります。
1
2
3
|
C = 2
NN = Chain(l1=L.Linear(N, C))
|
このニューラルネットワークを使った関数を定義します。
1
2
3
| def model(x):
y = NN.l1(x)
return y
|
上記で定義した関数でデータを分類します。
1
2
| ydata = model(xdata)
ydata
|

正解率を検証します。
1
2
3
|
acc = F.accuracy(ydata, tdata)
acc
|
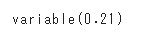
結果は0.21(21%)ととても低いですが、まったく学習をしていない状態なので気にする必要はありません。
ニューラルネットワークを最適化する手法を設定します。
1
2
3
|
optNN = Opt.SGD()
optNN.setup(NN)
|
結果を確認するために、誤差と正解率を記録するエリアを定義します。
1
2
3
|
loss_series = []
acc_series = []
|
いよいよ学習してみます。処理に関してはソースコメントを参照してください。
1
2
3
4
5
6
7
8
9
10
11
12
| T = 5000
for time in range(T):
config.train = True
optNN.target.zerograds()
ydata = model(xdata)
loss = F.softmax_cross_entropy(ydata, tdata)
acc= F.accuracy(ydata, tdata)
loss.backward()
optNN.update()
loss_series.append(loss.data)
acc_series.append(acc.data)
|
誤差がどのように変化しているかをグラフ化します。
1
2
3
4
5
6
7
8
9
10
|
Tall = len(loss_series)
plt.figure(figsize=(8, 6))
plt.plot(range(Tall), loss_series)
plt.title('loss function in training')
plt.xlabel('step')
plt.ylabel('loss function')
plt.xlim([0, Tall])
plt.ylim(0, 1)
plt.show()
|
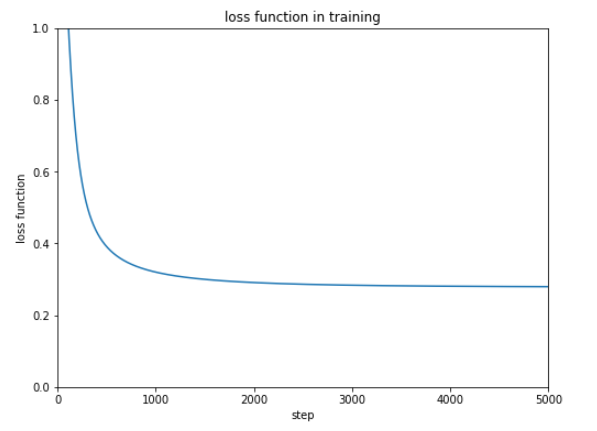
0.3付近までは順調に誤差が減っていますがそこからは改善していないようです。
次に、正解率の遷移をグラフ化します。
1
2
3
4
5
6
7
8
9
10
|
Tall = len(acc_series)
plt.figure(figsize=(8, 6))
plt.plot(range(Tall), acc_series)
plt.title('accuracy in training')
plt.xlabel('step')
plt.ylabel('accuracy')
plt.xlim([0, Tall])
plt.ylim(0, 1)
plt.show()
|
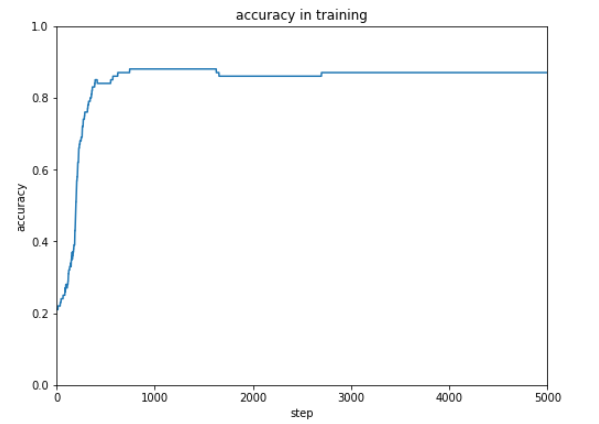
0.85(85%)付近までは上昇しますが、そこが限界のようです。
さらなる精度情報のために2層のニューラルネットワークにしてみます。
下記では、入力が2種類、中間層が4層、出力が2種類となるニューラルネットワークを定義しています。
1
2
3
|
C = 2
NN = Chain(l1=L.Linear(N, 4), l2=L.Linear(4 , C))
|
2層のニューラルネットワークの関数化ですが2つの線形変換の間に非線形変換をいれるとよいとのことです。
シグモイド関数をはさんでみました。
1
2
3
4
5
6
|
def model(x):
h = NN.l1(x)
h = F.sigmoid(h)
y = NN.l2(h)
return y
|
あらたにニューラルネットワークを定義したので、最適化手法を再設定します。
学習記録もいったん初期化し、学習を2万回に増やして実行します。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
optNN = Opt.SGD()
optNN.setup(NN)
loss_series = []
acc_series = []
T = 20000
for time in range(T):
config.train = True
optNN.target.zerograds()
ydata = model(xdata)
loss = F.softmax_cross_entropy(ydata, tdata)
acc= F.accuracy(ydata, tdata)
loss.backward()
optNN.update()
loss_series.append(loss.data)
acc_series.append(acc.data)
|
結果は下記のとおりです。
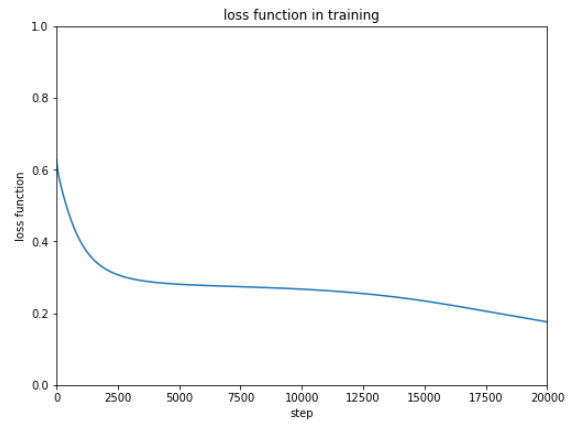
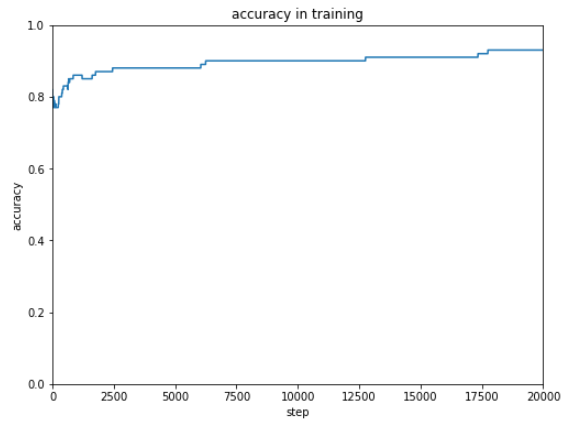
誤差の結果をみるとまだまだ改善するような感じなのでもう2万回 追加で学習をしてみます。
再実行するのは、ループの[学習]のところと[学習記録の表示(誤差)][学習記録の表示(正解率)]です。
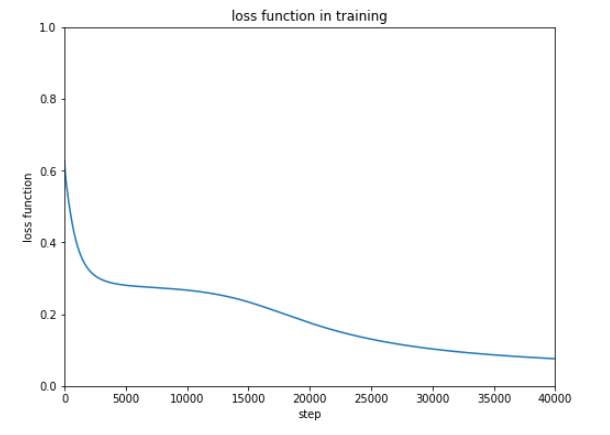
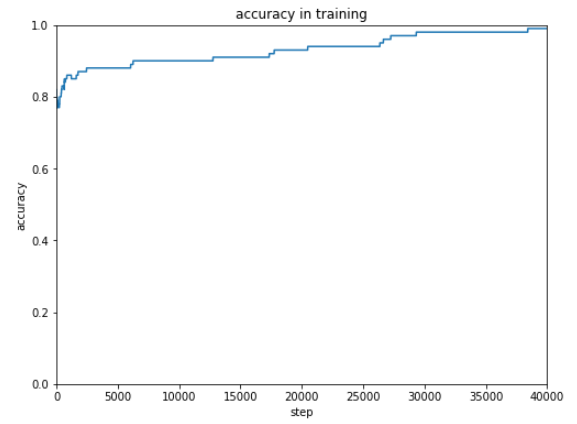
だんだん結果がよくなっているので、もう2万回追加で実行します。
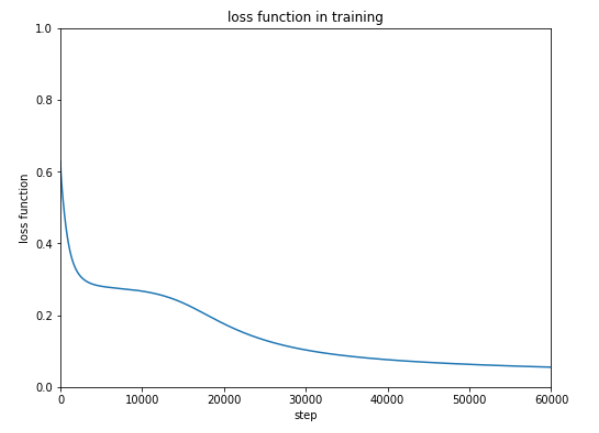
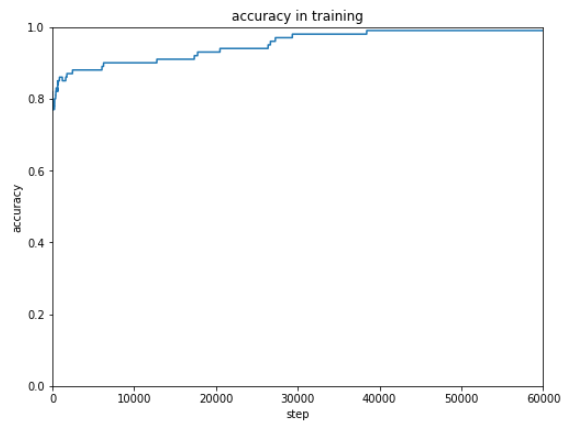
ほぼ100%の正解率にすることができました。
誤差が改善する見込みがある場合は、学習回数を単純に増やしていくといいみたいです。
(Google Colaboratoryで動作確認しています。)