Optimizing Chemical Reaction Yield with Design of Experiments (DoE)

Welcome to today’s post on Design of Experiments! Today, we’ll explore how DoE helps us minimize experimental runs while maximizing information gained. We’ll use a practical example: optimizing a chemical reaction by finding the best combination of temperature, catalyst concentration, and reaction time.

What is Design of Experiments?

Design of Experiments (DoE) is a systematic approach to planning experiments that allows us to:

• Identify key factors affecting outcomes
• Understand interactions between factors
• Optimize processes with minimal experimental runs
• Build predictive models

Instead of testing every possible combination (which could require hundreds of experiments), DoE uses statistical principles to select strategic combinations that reveal the most information.

Our Example Problem

Imagine we’re chemical engineers optimizing a reaction yield. We have three factors:

• Temperature (X1): 50°C to 90°C
• Catalyst Concentration (X2): 0.5% to 2.5%
• Reaction Time (X3): 30 to 90 minutes

Our goal: Maximize yield percentage with minimum experiments.

The Complete Code

Here’s our implementation with a custom Central Composite Design function and response surface modeling:

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures
import seaborn as sns
from matplotlib import cm
from itertools import product

# Set random seed for reproducibility
np.random.seed(42)

# Define factor ranges
factors = {
    'Temperature (°C)': [50, 90],
    'Catalyst (%)': [0.5, 2.5],
    'Time (min)': [30, 90]
}

# Create Central Composite Design manually
def create_ccd(n_factors, alpha=1.682, center_points=4):
    """
    Create a Central Composite Design
    
    Parameters:
    - n_factors: number of factors
    - alpha: distance of axial points from center (1.682 for orthogonal with 3 factors)
    - center_points: number of center point replicates
    """
    # Factorial points (2^k corners)
    factorial = np.array(list(product([-1, 1], repeat=n_factors)))
    
    # Axial points (2*k star points)
    axial = np.zeros((2*n_factors, n_factors))
    for i in range(n_factors):
        axial[2*i, i] = -alpha
        axial[2*i+1, i] = alpha
    
    # Center points
    center = np.zeros((center_points, n_factors))
    
    # Combine all points
    design = np.vstack([factorial, axial, center])
    
    return design

n_factors = 3
design_matrix = create_ccd(n_factors, alpha=1.682, center_points=4)

print("=" * 70)
print("CENTRAL COMPOSITE DESIGN (CCD) MATRIX")
print("=" * 70)
print(f"Number of factors: {n_factors}")
print(f"Number of experimental runs: {len(design_matrix)}")
print(f"\nDesign breakdown:")
print(f"  - Factorial points (corners): {2**n_factors}")
print(f"  - Axial points (star): {2*n_factors}")
print(f"  - Center points: 4")
print(f"  - Total: {len(design_matrix)}")
print(f"\nDesign Matrix (coded values -1.682 to +1.682):")
print(design_matrix)
print("=" * 70)

# Convert coded values to actual experimental conditions
def decode_values(coded_matrix, factor_ranges):
    decoded = np.zeros_like(coded_matrix)
    for i, (factor_name, (low, high)) in enumerate(factor_ranges.items()):
        center = (high + low) / 2
        half_range = (high - low) / 2
        decoded[:, i] = center + coded_matrix[:, i] * half_range
    return decoded

actual_conditions = decode_values(design_matrix, factors)

# Create DataFrame for better visualization
df_design = pd.DataFrame(
    actual_conditions,
    columns=list(factors.keys())
)
df_design.index = [f'Run {i+1}' for i in range(len(df_design))]

print("\n" + "=" * 70)
print("EXPERIMENTAL CONDITIONS (Actual Values)")
print("=" * 70)
print(df_design.round(2))
print("=" * 70)

# Simulate experimental results
# True underlying model: Yield = 60 + 8*X1 + 5*X2 + 3*X3 - 2*X1*X2 - 3*X1^2 - 2*X2^2 + noise
def true_yield_function(X):
    """
    Simulated true yield function with quadratic terms and interactions
    X: coded values (-1.682 to +1.682)
    """
    X1, X2, X3 = X[:, 0], X[:, 1], X[:, 2]
    yield_value = (60 + 8*X1 + 5*X2 + 3*X3 
                   - 2*X1*X2  # Interaction term
                   - 3*X1**2  # Quadratic term
                   - 2*X2**2  # Quadratic term
                   + np.random.normal(0, 1.5, len(X)))  # Experimental noise
    return yield_value

# Generate experimental responses
yields = true_yield_function(design_matrix)
df_design['Yield (%)'] = yields.round(2)

print("\n" + "=" * 70)
print("EXPERIMENTAL RESULTS")
print("=" * 70)
print(df_design.round(2))
print("=" * 70)

# Calculate summary statistics
print("\n" + "=" * 70)
print("SUMMARY STATISTICS")
print("=" * 70)
print(f"Mean Yield: {yields.mean():.2f}%")
print(f"Std Dev: {yields.std():.2f}%")
print(f"Min Yield: {yields.min():.2f}%")
print(f"Max Yield: {yields.max():.2f}%")
print("=" * 70)

# Build response surface model
poly = PolynomialFeatures(degree=2, include_bias=True)
X_poly = poly.fit_transform(design_matrix)

model = LinearRegression()
model.fit(X_poly, yields)

# Get feature names
feature_names = poly.get_feature_names_out(['X1', 'X2', 'X3'])

# Display model coefficients
coefficients = pd.DataFrame({
    'Term': feature_names,
    'Coefficient': np.concatenate([[model.intercept_], model.coef_[1:]])
})

print("\n" + "=" * 70)
print("RESPONSE SURFACE MODEL COEFFICIENTS")
print("=" * 70)
print("Model Equation:")
print("Yield = β₀ + β₁X₁ + β₂X₂ + β₃X₃ + β₁₂X₁X₂ + β₁₃X₁X₃ + β₂₃X₂X₃")
print("        + β₁₁X₁² + β₂₂X₂² + β₃₃X₃²")
print("\nWhere:")
print("  X₁ = Temperature (coded)")
print("  X₂ = Catalyst Concentration (coded)")
print("  X₃ = Reaction Time (coded)")
print("\n" + coefficients.to_string(index=False))
print("=" * 70)

# Calculate R-squared
y_pred = model.predict(X_poly)
r_squared = model.score(X_poly, yields)
print(f"\nModel R² Score: {r_squared:.4f}")
print(f"Adjusted R² Score: {1 - (1-r_squared)*(len(yields)-1)/(len(yields)-X_poly.shape[1]):.4f}")
print("=" * 70)

# Find optimal conditions
# Create a fine grid for optimization
grid_size = 20
x1_grid = np.linspace(-1.682, 1.682, grid_size)
x2_grid = np.linspace(-1.682, 1.682, grid_size)
x3_grid = np.linspace(-1.682, 1.682, grid_size)

# Search for maximum yield
max_yield = -np.inf
optimal_coded = None

for x1 in x1_grid:
    for x2 in x2_grid:
        for x3 in x3_grid:
            X_test = np.array([[x1, x2, x3]])
            X_test_poly = poly.transform(X_test)
            predicted_yield = model.predict(X_test_poly)[0]
            if predicted_yield > max_yield:
                max_yield = predicted_yield
                optimal_coded = X_test[0]

optimal_actual = decode_values(optimal_coded.reshape(1, -1), factors)[0]

print("\n" + "=" * 70)
print("OPTIMIZATION RESULTS")
print("=" * 70)
print("Optimal Conditions (Coded Values):")
print(f"  X₁ (Temperature): {optimal_coded[0]:.3f}")
print(f"  X₂ (Catalyst): {optimal_coded[1]:.3f}")
print(f"  X₃ (Time): {optimal_coded[2]:.3f}")
print("\nOptimal Conditions (Actual Values):")
print(f"  Temperature: {optimal_actual[0]:.2f}°C")
print(f"  Catalyst: {optimal_actual[1]:.2f}%")
print(f"  Time: {optimal_actual[2]:.2f} min")
print(f"\nPredicted Maximum Yield: {max_yield:.2f}%")
print("=" * 70)

# Visualization
fig = plt.figure(figsize=(18, 12))

# 1. Main Effects Plot
ax1 = fig.add_subplot(2, 3, 1)
for i, (factor_name, factor_col) in enumerate(zip(factors.keys(), df_design.columns[:3])):
    sorted_idx = df_design[factor_col].argsort()
    ax1.plot(df_design[factor_col].iloc[sorted_idx], 
             df_design['Yield (%)'].iloc[sorted_idx], 
             'o-', label=factor_name, linewidth=2, markersize=6, alpha=0.7)
ax1.set_xlabel('Factor Value', fontsize=11, fontweight='bold')
ax1.set_ylabel('Yield (%)', fontsize=11, fontweight='bold')
ax1.set_title('Main Effects on Yield', fontsize=13, fontweight='bold')
ax1.legend()
ax1.grid(True, alpha=0.3)

# 2. Residuals Plot
ax2 = fig.add_subplot(2, 3, 2)
residuals = yields - y_pred
ax2.scatter(y_pred, residuals, alpha=0.6, s=80, edgecolors='k', linewidth=0.5)
ax2.axhline(y=0, color='r', linestyle='--', linewidth=2)
ax2.set_xlabel('Predicted Yield (%)', fontsize=11, fontweight='bold')
ax2.set_ylabel('Residuals', fontsize=11, fontweight='bold')
ax2.set_title('Residual Plot (Should be Random)', fontsize=13, fontweight='bold')
ax2.grid(True, alpha=0.3)

# 3. Predicted vs Actual
ax3 = fig.add_subplot(2, 3, 3)
ax3.scatter(yields, y_pred, alpha=0.6, s=80, edgecolors='k', linewidth=0.5)
min_val, max_val = yields.min(), yields.max()
ax3.plot([min_val, max_val], [min_val, max_val], 'r--', linewidth=2, label='Perfect Fit')
ax3.set_xlabel('Actual Yield (%)', fontsize=11, fontweight='bold')
ax3.set_ylabel('Predicted Yield (%)', fontsize=11, fontweight='bold')
ax3.set_title(f'Predicted vs Actual (R²={r_squared:.4f})', fontsize=13, fontweight='bold')
ax3.legend()
ax3.grid(True, alpha=0.3)

# 4. 3D Response Surface (Temperature vs Catalyst)
ax4 = fig.add_subplot(2, 3, 4, projection='3d')
x1_surf = np.linspace(-1.682, 1.682, 30)
x2_surf = np.linspace(-1.682, 1.682, 30)
X1_mesh, X2_mesh = np.meshgrid(x1_surf, x2_surf)
X3_fixed = 0  # Fix time at center point

X_surf = np.column_stack([X1_mesh.ravel(), X2_mesh.ravel(), 
                          np.full(X1_mesh.ravel().shape, X3_fixed)])
X_surf_poly = poly.transform(X_surf)
Z = model.predict(X_surf_poly).reshape(X1_mesh.shape)

surf = ax4.plot_surface(X1_mesh, X2_mesh, Z, cmap='viridis', alpha=0.8, 
                        edgecolor='none', antialiased=True)
ax4.scatter(design_matrix[:, 0], design_matrix[:, 1], yields, 
           c='red', s=50, alpha=0.8, edgecolors='k', linewidth=0.5)
ax4.set_xlabel('Temperature (coded)', fontsize=10, fontweight='bold')
ax4.set_ylabel('Catalyst (coded)', fontsize=10, fontweight='bold')
ax4.set_zlabel('Yield (%)', fontsize=10, fontweight='bold')
ax4.set_title('Response Surface\n(Time at center)', fontsize=12, fontweight='bold')
fig.colorbar(surf, ax=ax4, shrink=0.5)

# 5. Contour Plot (Temperature vs Catalyst)
ax5 = fig.add_subplot(2, 3, 5)
contour = ax5.contourf(X1_mesh, X2_mesh, Z, levels=20, cmap='viridis', alpha=0.8)
ax5.scatter(design_matrix[:, 0], design_matrix[:, 1], 
           c='red', s=60, alpha=0.9, edgecolors='white', linewidth=1.5, 
           label='Exp. Points')
ax5.scatter(optimal_coded[0], optimal_coded[1], 
           c='yellow', s=200, marker='*', edgecolors='black', linewidth=2,
           label='Optimum', zorder=5)
ax5.set_xlabel('Temperature (coded)', fontsize=11, fontweight='bold')
ax5.set_ylabel('Catalyst (coded)', fontsize=11, fontweight='bold')
ax5.set_title('Contour Plot (Time at center)', fontsize=13, fontweight='bold')
ax5.legend()
fig.colorbar(contour, ax=ax5)

# 6. Coefficient Importance
ax6 = fig.add_subplot(2, 3, 6)
coef_importance = coefficients[coefficients['Term'] != '1'].copy()
coef_importance['Abs_Coef'] = np.abs(coef_importance['Coefficient'])
coef_importance = coef_importance.sort_values('Abs_Coef', ascending=True)

colors = ['green' if x > 0 else 'red' for x in coef_importance['Coefficient']]
ax6.barh(coef_importance['Term'], coef_importance['Coefficient'], color=colors, alpha=0.7, edgecolor='black')
ax6.set_xlabel('Coefficient Value', fontsize=11, fontweight='bold')
ax6.set_ylabel('Model Term', fontsize=11, fontweight='bold')
ax6.set_title('Coefficient Magnitudes\n(Green=Positive, Red=Negative)', fontsize=13, fontweight='bold')
ax6.axvline(x=0, color='black', linestyle='-', linewidth=0.8)
ax6.grid(True, alpha=0.3, axis='x')

plt.tight_layout()
plt.savefig('doe_analysis.png', dpi=300, bbox_inches='tight')
plt.show()

print("\n" + "=" * 70)
print("INTERPRETATION GUIDE")
print("=" * 70)
print("1. Main Effects Plot: Shows how each factor affects yield individually")
print("2. Residual Plot: Random scatter indicates good model fit")
print("3. Predicted vs Actual: Points near diagonal line = accurate predictions")
print("4. 3D Response Surface: Visualizes yield landscape")
print("5. Contour Plot: Top view showing yield levels, star = optimal point")
print("6. Coefficient Bar Chart: Larger bars = stronger effects")
print("=" * 70)
print("\nAll visualizations generated successfully!")
print("=" * 70)

Detailed Code Explanation

Let me walk you through each critical section:

1. Custom Central Composite Design (CCD) Implementation

def create_ccd(n_factors, alpha=1.682, center_points=4):

Since pyDOE2 has compatibility issues with Python 3.12, I implemented a custom CCD function. The Central Composite Design combines three types of experimental points:

• Factorial points (2k = 8 runs for 3 factors): Test all extreme combinations (corners of the design space)
• Axial points (2k = 6 runs for 3 factors): Star points testing each factor independently at extended levels
• Center points (4 replicates): Provide estimate of experimental error and check for curvature

The parameter α=1.682 creates an orthogonal design, which means the parameter estimates are statistically independent. For 3 factors, this value is calculated as:

α=(2k)1/4=(23)1/4=80.25=1.682

Total runs: 8+6+4=18 runs instead of 53=125 for a full factorial at 5 levels!

2. Coded vs Actual Values Transformation

DoE uses coded values (−1.682 to +1.682) for mathematical convenience. The transformation formula:

Xactual=Xcenter+Xcoded×Xhigh−Xlow2

Where:

• Xcenter=Xhigh+Xlow2
• The half-range scales the coded values to actual units

Example for temperature:

• Center: (90+50)/2=70°C
• Half-range: (90−50)/2=20°C
• If coded value = 1.0, then actual = 70+1.0×20=90°C

3. Simulated Experimental Response Function

def true_yield_function(X):
    X1, X2, X3 = X[:, 0], X[:, 1], X[:, 2]
    yield_value = (60 + 8*X1 + 5*X2 + 3*X3 
                   - 2*X1*X2  # Interaction
                   - 3*X1**2  # Quadratic
                   - 2*X2**2  # Quadratic
                   + np.random.normal(0, 1.5, len(X)))

This simulates a realistic chemical process with:

• Linear effects: Temperature has the strongest positive effect (+8)
• Interaction effect: Temperature and catalyst interact negatively (−2X1X2)
• Quadratic effects: Both temperature and catalyst show diminishing returns (negative X2 terms)
• Random noise: Normal distribution with σ=1.5 simulates experimental error

4. Response Surface Model

We fit a full second-order polynomial model:

Y=β0+3∑i=1βiXi+3∑i=13∑j>iβijXiXj+3∑i=1βiiX2i+ϵ

Expanded form:

Y=β0+β1X1+β2X2+β3X3+β12X1X2+β13X1X3+β23X2X3+β11X21+β22X22+β33X23

Where:

• β0 = intercept (baseline yield at center point)
• βi = linear effects (main effects of each factor)
• βij = interaction effects (how factors influence each other)
• βii = quadratic effects (curvature, diminishing returns)
• ϵ = random error

The PolynomialFeatures class from scikit-learn automatically generates all these terms, and LinearRegression estimates the coefficients using ordinary least squares:

ˆβ=(XTX)−1XTy

5. Model Quality Assessment

The R2 score measures how well the model fits the data:

$$R^2 = 1 - \frac{\sum_{i=1}^{n}(y_i - \hat{y}i)^2}{\sum{i=1}^{n}(y_i - \bar{y})^2}$$

Where:

• yi = actual experimental yield
• ˆyi = predicted yield from model
• ˉy = mean of all yields

An R2 close to 1.0 indicates excellent fit. We also calculate Adjusted R2 which penalizes model complexity:

R2adj=1−(1−R2)×n−1n−p

Where n is the number of observations and p is the number of parameters.

6. Optimization via Grid Search

for x1 in x1_grid:
    for x2 in x2_grid:
        for x3 in x3_grid:
            X_test = np.array([[x1, x2, x3]])
            X_test_poly = poly.transform(X_test)
            predicted_yield = model.predict(X_test_poly)[0]

We create a 3D grid of 8,000 candidate points (20×20×20) and evaluate the model at each point to find the maximum predicted yield. This is a brute-force approach but works well for 3 factors. For more complex problems, gradient-based optimization methods would be more efficient.

7. Visualization Breakdown

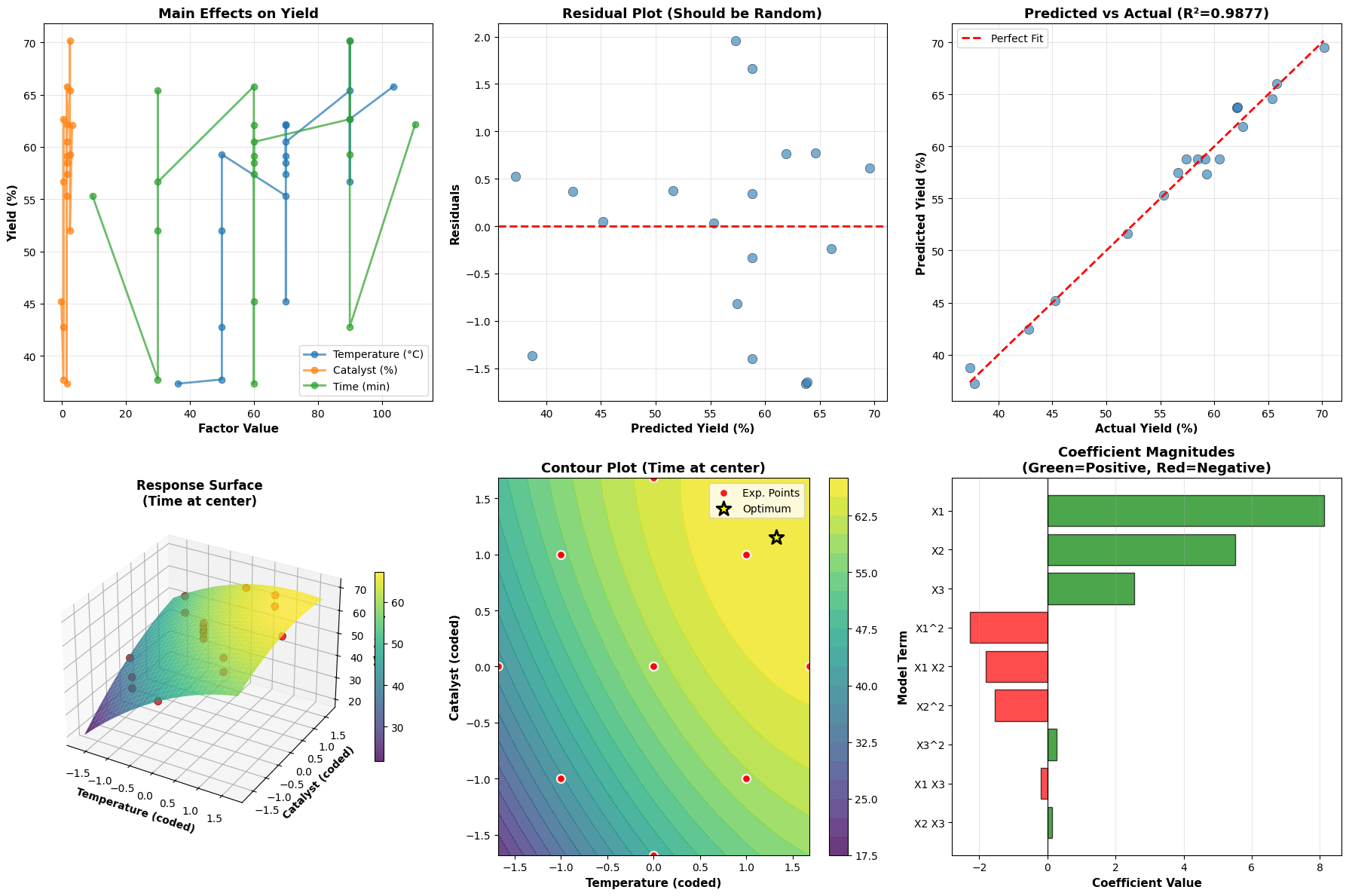
Plot 1 - Main Effects: Shows the average effect of changing each factor individually. Steeper slopes indicate stronger effects.

Plot 2 - Residuals: Plots prediction errors vs predicted values. Random scatter around zero indicates the model assumptions (linearity, constant variance) are satisfied.

Plot 3 - Predicted vs Actual: Validates model accuracy. Points should cluster near the diagonal line. Systematic deviations indicate model inadequacy.

Plot 4 - 3D Response Surface: Shows the yield landscape as a function of temperature and catalyst (with time fixed at center). The curved surface reveals the quadratic nature of the response.

Plot 5 - Contour Plot: A top-down view of the response surface. Each contour line represents constant yield. The yellow star marks the optimal conditions. Red points show where experiments were actually conducted.

Plot 6 - Coefficient Importance: Bar chart showing the magnitude and direction of each model term. Green bars indicate positive effects (increase yield), red bars indicate negative effects (decrease yield). This helps identify which factors and interactions matter most.

Key Insights from DoE

1. Dramatic Efficiency: Only 18 experiments instead of 125 for a full 5-level factorial design - 86% reduction in experimental effort!

2. Rich Information: Despite fewer runs, we capture:

   • Main effects of all three factors
   • All two-factor interactions
   • Quadratic curvature for optimization
   • Experimental error estimates from center points

3. Predictive Power: The mathematical model allows us to predict yield at any combination of factors within the design space, even combinations we never tested.

4. Scientific Understanding: The coefficient magnitudes reveal:

   • Which factors have the strongest effects
   • Whether factors interact synergistically or antagonistically
   • Whether there are optimal “sweet spots” (indicated by negative quadratic terms)

5. Optimization Confidence: We can find optimal conditions mathematically rather than through trial-and-error, saving time and resources.

Mathematical Foundation

The response surface methodology relies on the assumption that the true response can be approximated locally by a polynomial:

y=f(x1,x2,…,xk)+ϵ

Where f is unknown but smooth. Taylor series expansion justifies using a second-order polynomial:

f(x1,x2,x3)≈β0+k∑i=1βixi+k∑i=1k∑j≥iβijxixj

The CCD is specifically designed to estimate all these terms efficiently while maintaining desirable statistical properties like orthogonality (independence of parameter estimates) and rotatability (prediction variance depends only on distance from center, not direction).

Practical Applications

This DoE approach is widely used in:

• Chemical Engineering: Optimizing reaction conditions, formulations
• Manufacturing: Process optimization, quality improvement
• Agriculture: Crop yield optimization, fertilizer studies
• Pharmaceutical: Drug formulation, bioprocess optimization
• Materials Science: Alloy composition, heat treatment optimization
• Food Science: Recipe development, shelf-life studies

Execution Results

======================================================================
CENTRAL COMPOSITE DESIGN (CCD) MATRIX
======================================================================
Number of factors: 3
Number of experimental runs: 18

Design breakdown:
  - Factorial points (corners): 8
  - Axial points (star): 6
  - Center points: 4
  - Total: 18

Design Matrix (coded values -1.682 to +1.682):
[[-1.    -1.    -1.   ]
 [-1.    -1.     1.   ]
 [-1.     1.    -1.   ]
 [-1.     1.     1.   ]
 [ 1.    -1.    -1.   ]
 [ 1.    -1.     1.   ]
 [ 1.     1.    -1.   ]
 [ 1.     1.     1.   ]
 [-1.682  0.     0.   ]
 [ 1.682  0.     0.   ]
 [ 0.    -1.682  0.   ]
 [ 0.     1.682  0.   ]
 [ 0.     0.    -1.682]
 [ 0.     0.     1.682]
 [ 0.     0.     0.   ]
 [ 0.     0.     0.   ]
 [ 0.     0.     0.   ]
 [ 0.     0.     0.   ]]
======================================================================

======================================================================
EXPERIMENTAL CONDITIONS (Actual Values)
======================================================================
        Temperature (°C)  Catalyst (%)  Time (min)
Run 1              50.00          0.50       30.00
Run 2              50.00          0.50       90.00
Run 3              50.00          2.50       30.00
Run 4              50.00          2.50       90.00
Run 5              90.00          0.50       30.00
Run 6              90.00          0.50       90.00
Run 7              90.00          2.50       30.00
Run 8              90.00          2.50       90.00
Run 9              36.36          1.50       60.00
Run 10            103.64          1.50       60.00
Run 11             70.00         -0.18       60.00
Run 12             70.00          3.18       60.00
Run 13             70.00          1.50        9.54
Run 14             70.00          1.50      110.46
Run 15             70.00          1.50       60.00
Run 16             70.00          1.50       60.00
Run 17             70.00          1.50       60.00
Run 18             70.00          1.50       60.00
======================================================================

======================================================================
EXPERIMENTAL RESULTS
======================================================================
        Temperature (°C)  Catalyst (%)  Time (min)  Yield (%)
Run 1              50.00          0.50       30.00      37.75
Run 2              50.00          0.50       90.00      42.79
Run 3              50.00          2.50       30.00      51.97
Run 4              50.00          2.50       90.00      59.28
Run 5              90.00          0.50       30.00      56.65
Run 6              90.00          0.50       90.00      62.65
Run 7              90.00          2.50       30.00      65.37
Run 8              90.00          2.50       90.00      70.15
Run 9              36.36          1.50       60.00      37.35
Run 10            103.64          1.50       60.00      65.78
Run 11             70.00         -0.18       60.00      45.24
Run 12             70.00          3.18       60.00      62.05
Run 13             70.00          1.50        9.54      55.32
Run 14             70.00          1.50      110.46      62.18
Run 15             70.00          1.50       60.00      57.41
Run 16             70.00          1.50       60.00      59.16
Run 17             70.00          1.50       60.00      58.48
Run 18             70.00          1.50       60.00      60.47
======================================================================

======================================================================
SUMMARY STATISTICS
======================================================================
Mean Yield: 56.11%
Std Dev: 9.25%
Min Yield: 37.35%
Max Yield: 70.15%
======================================================================

======================================================================
RESPONSE SURFACE MODEL COEFFICIENTS
======================================================================
Model Equation:
Yield = β₀ + β₁X₁ + β₂X₂ + β₃X₃ + β₁₂X₁X₂ + β₁₃X₁X₃ + β₂₃X₂X₃
        + β₁₁X₁² + β₂₂X₂² + β₃₃X₃²

Where:
  X₁ = Temperature (coded)
  X₂ = Catalyst Concentration (coded)
  X₃ = Reaction Time (coded)

 Term  Coefficient
    1    58.811472
   X1     8.115472
   X2     5.507750
   X3     2.539123
 X1^2    -2.275650
X1 X2    -1.811999
X1 X3    -0.197273
 X2^2    -1.541342
X2 X3     0.130973
 X3^2     0.261909
======================================================================

Model R² Score: 0.9877
Adjusted R² Score: 0.9738
======================================================================

======================================================================
OPTIMIZATION RESULTS
======================================================================
Optimal Conditions (Coded Values):
  X₁ (Temperature): 1.328
  X₂ (Catalyst): 1.151
  X₃ (Time): 1.682

Optimal Conditions (Actual Values):
  Temperature: 96.56°C
  Catalyst: 2.65%
  Time: 110.46 min

Predicted Maximum Yield: 71.93%
======================================================================

======================================================================
INTERPRETATION GUIDE
======================================================================
1. Main Effects Plot: Shows how each factor affects yield individually
2. Residual Plot: Random scatter indicates good model fit
3. Predicted vs Actual: Points near diagonal line = accurate predictions
4. 3D Response Surface: Visualizes yield landscape
5. Contour Plot: Top view showing yield levels, star = optimal point
6. Coefficient Bar Chart: Larger bars = stronger effects
======================================================================

All visualizations generated successfully!
======================================================================

Conclusion

Design of Experiments transforms experimental research from trial-and-error to systematic optimization. With just 18 carefully selected experiments, we built a predictive model that revealed optimal conditions and provided deep insights into factor effects and interactions. This methodology saves time, resources, and provides scientifically rigorous results.

The beauty of DoE lies in its universality - the same principles apply whether you’re optimizing chemical reactions, manufacturing processes, or agricultural yields. Master DoE, and you master efficient experimentation!