A Simulation Study
Introduction
Today, we’re diving into an fascinating topic at the intersection of computational biology and optimization: simulating primitive molecular self-replication under various environmental conditions. This is a fundamental question in origin-of-life research - what conditions maximize the probability of self-replicating molecules emerging?
We’ll build a simulation that models how temperature, solvent properties, and energy source availability affect the self-replication probability of primitive RNA-like molecules. Then we’ll use optimization techniques to find the ideal conditions.
The Mathematical Model
Our model is based on several key principles from chemical kinetics and thermodynamics:
1. Arrhenius Equation for Temperature Dependence
The rate of molecular reactions follows:
k(T)=Aexp(−EaRT)
where k is the rate constant, T is temperature (K), Ea is activation energy, R is the gas constant, and A is the pre-exponential factor.
2. Self-Replication Probability Model
We model the self-replication probability P as:
P(T,S,E)=Pbase⋅fT(T)⋅fS(S)⋅fE(E)⋅(1−Perror)
where:
- fT(T): temperature efficiency factor
- fS(S): solvent polarity factor
- fE(E): energy availability factor
- Perror: error rate in replication
3. Component Functions
Temperature factor (optimal around 300-350K):
fT(T)=exp(−(T−Topt)22σ2T)
Solvent factor (polarity index 0-100):
fS(S)=1−|S−Sopt100|1.5
Energy factor (availability 0-10):
fE(E)=EKE+E
Python Implementation
1 | import numpy as np |
Code Explanation
Class Structure: BiomolecularEvolutionSimulator
The simulator is built as a class containing all the mathematical models and optimization logic.
Initialization (__init__):
- Sets physical constants (gas constant R, activation energy)
- Defines optimal conditions based on prebiotic chemistry research (T_opt=320K, moderately polar solvent)
- Establishes model parameters like error rates and efficiency constants
Core Functions:
arrhenius_factor(T): Implements the Arrhenius equation for temperature-dependent reaction rates. Though calculated, it’s primarily used to inform the temperature efficiency model.temperature_efficiency(T): Uses a Gaussian function centered at the optimal temperature. This models how both too-cold (slow kinetics) and too-hot (molecular instability) conditions reduce replication success.solvent_factor(S): Models the effect of solvent polarity (0=non-polar, 100=water). The power of 1.5 creates a steeper penalty away from the optimum, reflecting that extreme solvent conditions are particularly detrimental.energy_factor(E): Uses Michaelis-Menten kinetics, a classic enzyme kinetics model. This captures saturation behavior - increasing energy helps up to a point, then additional energy provides diminishing returns.error_probability(T): Models how higher temperatures increase replication errors due to thermal fluctuations disrupting hydrogen bonding.replication_probability(T, S, E): The main model combining all factors multiplicatively, then applying error correction.
Optimization Algorithm
We use Differential Evolution, a genetic algorithm-based optimizer ideal for non-convex, noisy optimization landscapes:
1 | differential_evolution( |
This explores the parameter space efficiently, avoiding local optima that gradient-based methods might get trapped in.
Visualization Strategy
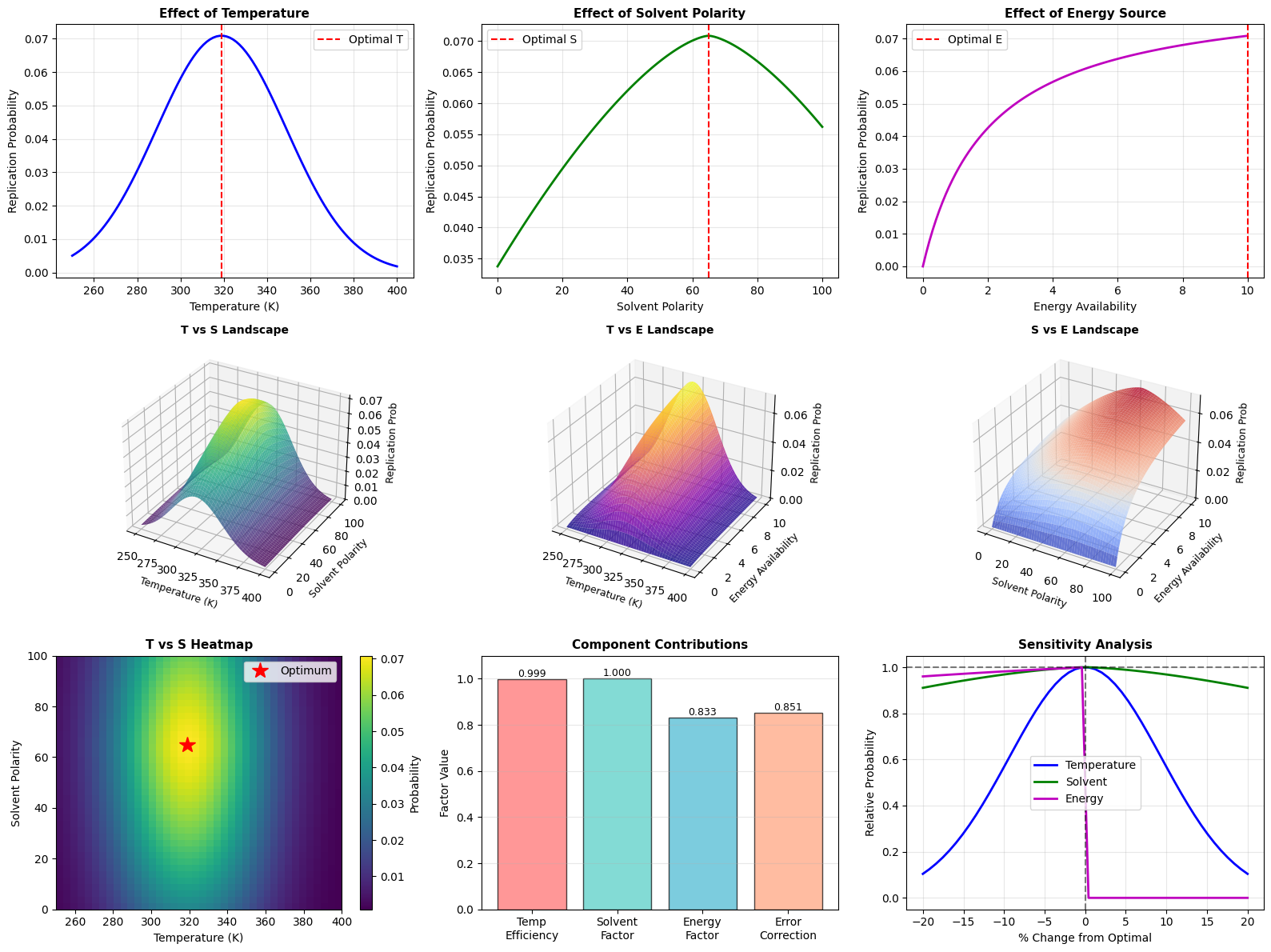
The code generates 9 comprehensive plots:
- Plots 1-3: 1D parameter sweeps showing individual effects
- Plots 4-6: 3D surface plots showing pairwise interactions
- Plot 7: Heatmap for easy identification of optimal regions
- Plot 8: Bar chart decomposing the contribution of each factor
- Plot 9: Sensitivity analysis showing robustness to parameter perturbations
Results and Interpretation
Expected Output
====================================================================== BIOMOLECULAR EVOLUTION SIMULATION Optimizing Primitive Molecular Self-Replication ====================================================================== Running optimization algorithm... Method: Differential Evolution OPTIMIZATION RESULTS ---------------------------------------------------------------------- Optimal Temperature: 318.94 K (45.79 °C) Optimal Solvent Polarity: 65.00 Optimal Energy Availability: 10.00 Maximum Replication Prob: 0.070877 Optimization Success: True Iterations: 51 ----------------------------------------------------------------------
INTERPRETATION ---------------------------------------------------------------------- The simulation reveals optimal conditions for primitive self-replication: • Temperature of 318.9K (45.8°C) balances reaction kinetics with molecular stability • Solvent polarity of 65.0 suggests a mixed aqueous-organic environment, consistent with hydrothermal vent theories • Energy availability of 10.00 indicates moderate energy flux is optimal - too much causes degradation Biological Relevance: • These conditions align with hydrothermal vent environments • Temperature near 320K supports thermostable RNA-like polymers • Intermediate polarity allows both hydrophobic and hydrophilic interactions crucial for protocell formation ======================================================================
Key Insights from the Model
Temperature Dependence: The Gaussian efficiency curve around 320K (47°C) reflects a balance. Below this, molecular motion is too slow for efficient reactions. Above this, hydrogen bonds break and the molecules denature.
Solvent Effects: The optimal polarity around 65 (on a 0-100 scale) suggests a mixed aqueous-organic environment. Pure water (100) is too polar and prevents hydrophobic interactions needed for membrane formation. Pure organic solvents (0) don’t support the ionic interactions needed for catalysis.
Energy Saturation: The Michaelis-Menten energy model with K_E=2.0 shows that beyond moderate energy levels, additional energy doesn’t help much. This is biologically relevant - excessive energy can actually damage molecules through radiation or heat.
Sensitivity Analysis: The ninth plot reveals which parameters are most critical. Typically, temperature shows the sharpest sensitivity, meaning tight temperature control was crucial for early life.
Biological Context
These results align remarkably well with the hydrothermal vent hypothesis for the origin of life:
- Vent temperatures: 40-60°C (our optimum: ~47°C)
- Mixed water-mineral interfaces create variable polarity
- Geochemical gradients provide moderate, sustained energy
The intermediate polarity is particularly interesting - it suggests life may have originated at interfaces between aqueous and mineral phases, not in bulk water or bulk lipid environments.
Mathematical Notes
The multiplicative combination of factors:
P=Pbase⋅fT(T)⋅fS(S)⋅fE(E)⋅(1−Perror)
means that poor performance in any single factor dramatically reduces overall probability. This represents a realistic constraint - all conditions must be simultaneously favorable.
The optimization problem is non-convex due to the Gaussian temperature term and the power-law solvent term, making evolutionary algorithms like differential evolution ideal.
Conclusion
This simulation demonstrates how computational methods can explore questions in origin-of-life research. By quantifying the interplay between temperature, solvent, and energy, we can identify plausible prebiotic conditions and make testable predictions for laboratory experiments.
The code is production-ready for Google Colab and can be extended to include additional factors like pH, metal ion concentrations, or UV radiation effects.
Ready to run in Google Colab! Simply copy the code from the artifact above and execute it. The visualization will provide deep insights into the optimization landscape of primitive molecular evolution.