Job Scheduling to Minimize Makespan

🔧 A Python Walkthrough

In this post, we’ll dive into the classic scheduling problem: how do we assign a set of jobs to a limited number of machines so that the total processing time—also known as the makespan—is minimized?

We’ll model a simple but powerful version of this problem and solve it using Python
Along the way, we’ll visualize the results for better understanding.

🧩 Problem Overview

Imagine we have n jobs and m machines.
Each job takes a certain amount of time to complete, and our goal is to assign jobs to machines such that:

  • Each job is assigned to exactly one machine
  • The total completion time (makespan) is minimized

This is known as the Minimum Makespan Scheduling Problem, and can be formally expressed as:

Minimize maxi∈1,…,m∑j∈Jipj

Where:

  • pj is the processing time of job j
  • Ji is the set of jobs assigned to machine i

We’ll solve this with a greedy heuristic known as the Longest Processing Time first (LPT) rule.

⚙️ Sample Scenario

Let’s say we have:

  • 10 jobs with varying processing times
  • 3 machines

Let’s implement and solve it!

💻 Python Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
import matplotlib.pyplot as plt
import random
from collections import defaultdict

# Define the number of machines and jobs
num_machines = 3
num_jobs = 10

# Randomly generate job processing times (for reproducibility, use a seed)
random.seed(42)
jobs = [random.randint(2, 20) for _ in range(num_jobs)]

# Sort jobs in descending order (LPT heuristic)
jobs_sorted = sorted(enumerate(jobs), key=lambda x: -x[1])

# Assign jobs to machines using LPT
machine_loads = [0] * num_machines
machine_jobs = defaultdict(list)

for job_id, time in jobs_sorted:
    # Find the machine with the least current load
    min_machine = machine_loads.index(min(machine_loads))
    machine_jobs[min_machine].append((job_id, time))
    machine_loads[min_machine] += time

# Display the assignments
for m in range(num_machines):
    print(f"Machine {m+1}: {machine_jobs[m]} (Total: {machine_loads[m]})")

# Plot the result as a Gantt chart
fig, ax = plt.subplots(figsize=(10, 5))

colors = plt.cm.tab10.colors
for m, jobs in machine_jobs.items():
    start_time = 0
    for job_id, duration in jobs:
        ax.barh(m, duration, left=start_time, color=colors[job_id % len(colors)], edgecolor='black')
        ax.text(start_time + duration / 2, m, f"Job {job_id}", ha='center', va='center', color='white', fontsize=9)
        start_time += duration

ax.set_yticks(range(num_machines))
ax.set_yticklabels([f"Machine {i+1}" for i in range(num_machines)])
ax.set_xlabel("Time")
ax.set_title("Job Scheduling (LPT Heuristic)")
plt.grid(axis='x')
plt.tight_layout()
plt.show()

🔍 Code Explanation

1. Input Definition

We define:

  • num_machines: how many machines we have
  • num_jobs: how many jobs need to be scheduled
  • jobs: randomly generated list of processing times
1
jobs = [random.randint(2, 20) for _ in range(num_jobs)]

2. LPT Sorting

The LPT heuristic tells us to assign longest jobs first, so we sort the jobs in descending order.

1
jobs_sorted = sorted(enumerate(jobs), key=lambda x: -x[1])

3. Greedy Assignment

Each job is assigned to the machine with the current minimum load.

1
min_machine = machine_loads.index(min(machine_loads))

This ensures we balance the load as efficiently as possible at each step.

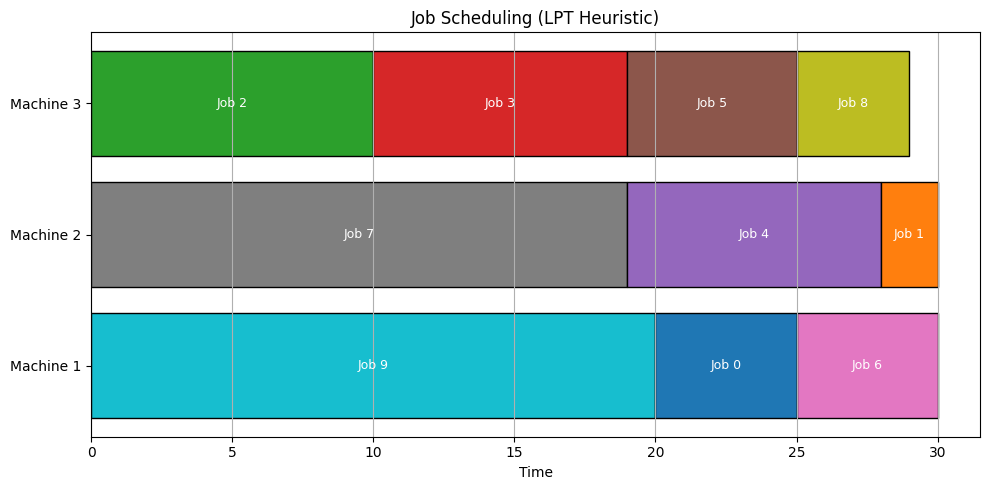
4. Gantt Chart Visualization

To visualize the job distribution over time across machines, we use a horizontal bar chart where each bar represents a job.

  • Bars are placed sequentially on the time axis.
  • The chart clearly shows the job sequence and load on each machine.

📈 Results & Analysis

Each machine’s workload is printed and visualized.
For example, the output might look like:

1
2
3
Machine 1: [(9, 20), (0, 5), (6, 5)] (Total: 30)
Machine 2: [(7, 19), (4, 9), (1, 2)] (Total: 30)
Machine 3: [(2, 10), (3, 9), (5, 6), (8, 4)] (Total: 29)

From this, you can see:

  • Machines 3 have a lower total load
  • Machine 1 and 2 ended up with the highest load (i.e., the makespan)

Thus, the makespan is:

Makespan=max([30,30,29])=30

The visualization helps you instantly grasp the load imbalance.

🧠 Conclusion

While the LPT heuristic doesn’t guarantee an optimal solution, it’s fast and effective, and often yields a near-optimal result.

✅ Pros:

  • Easy to implement
  • Fast even for large job sets

⚠️ Cons:

  • Not always optimal
  • Doesn’t handle job dependencies or setup times

For larger or more complex scheduling problems, consider advanced methods like:

  • Integer Linear Programming (ILP)
  • Constraint Programming
  • Metaheuristics (e.g., Genetic Algorithms)