Designing a Network with Minimum Cost

🕸️ A Python Guide to Minimum Spanning Trees

When you’re designing a network — whether it’s connecting computers, cities, or pipelines — you often want to connect all nodes with the lowest possible cost.
This is the heart of the Minimum Spanning Tree (MST) problem in graph theory.

Today, we’ll solve an MST problem using Python in a Google Colab environment, leveraging Kruskal’s Algorithm and visualizing the result with networkx and matplotlib.

🌐 The Scenario: Connecting Cities

Imagine you’re tasked with connecting 7 cities with network cables.
You’re given a list of possible cable routes and the cost of each connection.
Your goal is to connect all cities using the least total cable cost, ensuring that the network remains connected (no isolated cities) and no cycles (loops) are formed.

Here’s our list of cities and connection costs:

City A City B Cost
A B 7
A D 5
B C 8
B D 9
B E 7
C E 5
D E 15
D F 6
E F 8
E G 9
F G 11

🧮 Mathematical Definition

Given an undirected graph G=(V,E), where:

  • V: set of vertices (cities)
  • E: set of edges with weights (costs)

Find a subset T⊆E such that:

  • T connects all vertices (spanning)
  • T contains no cycles (tree)
  • The sum of edge weights in T is minimized

Mathematically, minimize:

∑(u,v)∈Tw(u,v)

🧑‍💻 Python Code: Kruskal’s Algorithm

Let’s implement Kruskal’s Algorithm to solve this MST problem.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
import networkx as nx
import matplotlib.pyplot as plt

# Define the graph edges and their weights
edges = [
    ("A", "B", 7),
    ("A", "D", 5),
    ("B", "C", 8),
    ("B", "D", 9),
    ("B", "E", 7),
    ("C", "E", 5),
    ("D", "E", 15),
    ("D", "F", 6),
    ("E", "F", 8),
    ("E", "G", 9),
    ("F", "G", 11)
]

# Create an undirected graph
G = nx.Graph()
G.add_weighted_edges_from(edges)

# Use Kruskal's algorithm to compute the Minimum Spanning Tree
mst = nx.minimum_spanning_tree(G, algorithm="kruskal")

# Display MST edges and total cost
print("Edges in MST:")
total_cost = 0
for u, v, data in mst.edges(data=True):
    print(f"{u} - {v}: {data['weight']}")
    total_cost += data['weight']
print(f"\nTotal Cost of MST: {total_cost}")

🧠 Code Explanation

  • networkx.Graph(): Initializes an undirected graph.
  • add_weighted_edges_from(edges): Adds edges with costs (weights).
  • minimum_spanning_tree(..., algorithm="kruskal"): Runs Kruskal’s algorithm.
  • The MST edges and their weights are printed along with the total cost.

📊 Visualizing the Network

Let’s visualize both the original graph and the resulting MST.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
# Position nodes using spring layout for clarity
pos = nx.spring_layout(G, seed=42)

# Draw original graph in light gray
plt.figure(figsize=(12, 6))
plt.subplot(1, 2, 1)
nx.draw(G, pos, with_labels=True, node_color='lightblue', node_size=800, edge_color='gray')
nx.draw_networkx_edge_labels(G, pos, edge_labels={(u,v): d['weight'] for u,v,d in G.edges(data=True)})
plt.title("Original Graph")

# Draw MST in second subplot
plt.subplot(1, 2, 2)
nx.draw(G, pos, with_labels=True, node_color='lightblue', node_size=800, edge_color='lightgray')
nx.draw(mst, pos, with_labels=True, node_color='lightgreen', node_size=800, edge_color='green', width=2)
nx.draw_networkx_edge_labels(mst, pos, edge_labels={(u,v): d['weight'] for u,v,d in mst.edges(data=True)})
plt.title("Minimum Spanning Tree")

plt.tight_layout()
plt.show()

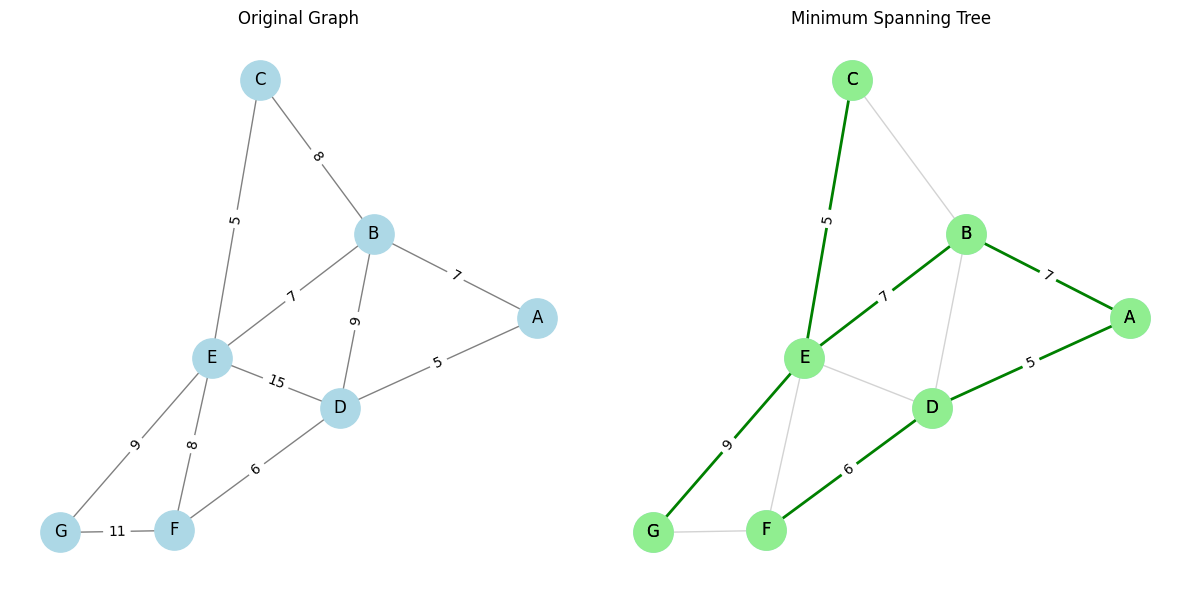
🔍 Visual Result Analysis

Edges in MST:
A - D: 5
A - B: 7
B - E: 7
D - F: 6
C - E: 5
E - G: 9

Total Cost of MST: 39

  • In the left graph, all possible connections and costs are visible.
  • In the right graph, only the optimal (cheapest) connections forming the MST are shown in green.
  • The MST does not contain any cycles and connects all 7 cities.
  • This is the most efficient way to lay cables with a total cost of 39.

✅ Conclusion

The Minimum Spanning Tree is a powerful tool in network design, ensuring all points are connected at the lowest possible cost without redundancies.
Using networkx, we efficiently solved and visualized the MST problem in Python.

Whether you’re building data centers, road networks, or even game maps — understanding MSTs can help you make smart, cost-effective decisions.