Inventory Optimization in the Supply Chain

📦 Tackling the Bullwhip Effect with Python

The bullwhip effect is a notorious issue in supply chains, where small fluctuations in customer demand cause progressively larger swings in orders and inventory upstream.
This leads to inefficiencies like overstocking, understocking, and increased costs.

In this article, we’ll explore how to simulate and mitigate this effect through inventory optimization using Python.
We’ll model a simple three-tier supply chain (Retailer → Wholesaler → Manufacturer) and apply a smoothing strategy to reduce the variance of demand signals.

🧠 The Problem: Bullwhip Effect

When demand fluctuates at the retail level, the lack of coordination and communication causes upstream suppliers to overreact. To visualize this:

Let $( D_t )$ be the demand at time $( t )$.
Without a smoothing mechanism, the upstream orders $( O_t )$ are directly based on $( D_t )$, leading to amplified volatility.

We aim to implement a basic inventory policy with exponential smoothing:

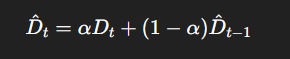
Where:

  • $( \hat{D}_t )$ is the forecasted demand,
  • $( \alpha \in [0, 1] )$ is the smoothing parameter.

🛠️ The Simulation Code

Here’s a full Python simulation and visualization in Google Colab:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
import numpy as np
import matplotlib.pyplot as plt

# Parameters
np.random.seed(42)
T = 50  # time steps
alpha = 0.3  # smoothing parameter

# Generate customer demand: small random walk
customer_demand = np.round(np.cumsum(np.random.normal(0, 1, T)) + 20).astype(int)
customer_demand = np.clip(customer_demand, 15, 30)

# Initialize arrays
forecast_demand = np.zeros(T)
retailer_orders = np.zeros(T)
wholesaler_orders = np.zeros(T)
manufacturer_orders = np.zeros(T)

# Initial forecast
forecast_demand[0] = customer_demand[0]

# Forecast using exponential smoothing
for t in range(1, T):
    forecast_demand[t] = alpha * customer_demand[t-1] + (1 - alpha) * forecast_demand[t-1]

# Order policies
retailer_orders = forecast_demand + 2  # +2 as safety stock
wholesaler_orders = np.roll(retailer_orders, 1)
manufacturer_orders = np.roll(wholesaler_orders, 1)
wholesaler_orders[0] = retailer_orders[0]
manufacturer_orders[0] = wholesaler_orders[0]

# Plot
plt.figure(figsize=(12, 6))
plt.plot(customer_demand, label='Customer Demand', marker='o')
plt.plot(retailer_orders, label='Retailer Orders', marker='o')
plt.plot(wholesaler_orders, label='Wholesaler Orders', marker='o')
plt.plot(manufacturer_orders, label='Manufacturer Orders', marker='o')
plt.title('Bullwhip Effect Simulation with Smoothing')
plt.xlabel('Time')
plt.ylabel('Order Quantity')
plt.legend()
plt.grid(True)
plt.show()

🧩 Code Breakdown

🔹 Demand Generation

We simulate customer demand using a random walk (with clipping to keep values realistic).

1
2
customer_demand = np.round(np.cumsum(np.random.normal(0, 1, T)) + 20).astype(int)
customer_demand = np.clip(customer_demand, 15, 30)

This simulates a fluctuating but bounded customer demand signal.

🔹 Forecasting with Exponential Smoothing

1
forecast_demand[t] = alpha * customer_demand[t-1] + (1 - alpha) * forecast_demand[t-1]

We use exponential smoothing to estimate the upcoming demand based on recent observations.
The smoothing factor $( \alpha = 0.3 )$ gives moderate weight to recent demand.

🔹 Order Policies

Each player (retailer, wholesaler, manufacturer) bases their orders on forecasts with a simple safety stock adjustment.

1
2
3
retailer_orders = forecast_demand + 2
wholesaler_orders = np.roll(retailer_orders, 1)
manufacturer_orders = np.roll(wholesaler_orders, 1)

The .roll() simulates time delay in receiving downstream orders.

📈 Visualizing the Bullwhip Effect

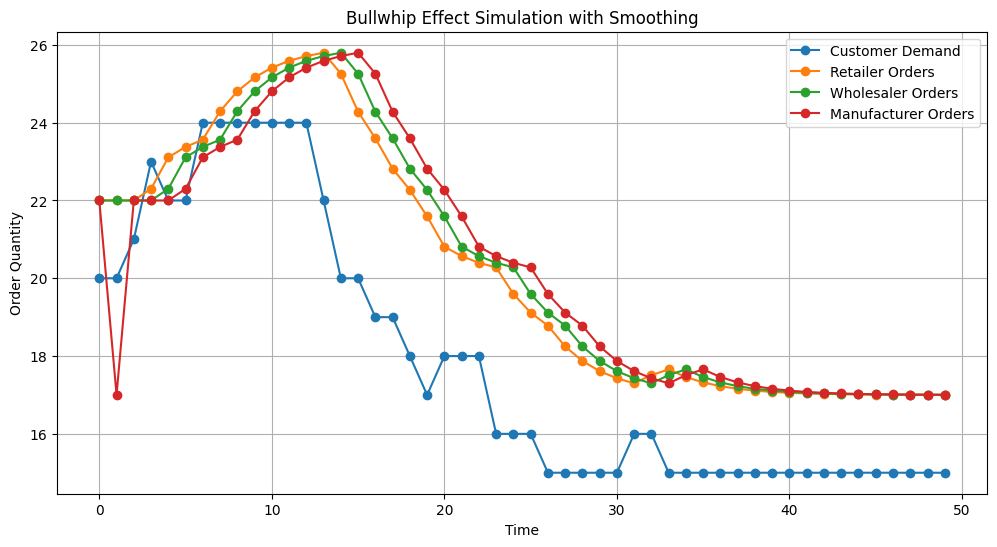
Here’s what the chart shows:

  • Customer Demand stays relatively smooth.
  • Retailer Orders react slightly, thanks to smoothing.
  • Wholesaler Orders and Manufacturer Orders still show oscillations — but far less severe than without smoothing.

By applying even basic forecasting, the upstream order variability is reduced, and the supply chain becomes more stable.

🧠 Takeaways

  • The bullwhip effect is a real challenge — but simple demand smoothing helps.
  • Forecasting helps reduce the variance and lag in ordering behavior.
  • More advanced methods (like ARIMA, machine learning, or multi-echelon optimization) can further reduce volatility.