Advanced Fluid Dynamics Simulation

A Python-Based Study of Pipe Flow and Pressure Drop Analysis

I’ll create a example of fluid dynamics, this time focusing on pipe flow analysis using the $Hagen$-$Poiseuille$ equation and pressure drop calculations.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import fsolve

class PipeFlowAnalyzer:
    def __init__(self):
        # Fluid properties (water at 20°C)
        self.density = 998.2      # kg/m³
        self.viscosity = 0.001    # Pa·s
        
        # Pipe properties
        self.length = 10.0        # m
        self.diameter = 0.05      # m
        self.roughness = 0.0015   # mm (typical for commercial steel)
        
    def reynolds_number(self, velocity):
        """Calculate Reynolds number"""
        return self.density * velocity * self.diameter / self.viscosity
    
    def friction_factor(self, reynolds):
        """
        Calculate Darcy friction factor using Colebrook-White equation
        """
        def colebrook(f):
            return (1/np.sqrt(f) + 2.0*np.log10(self.roughness/(3.7*self.diameter*1000) + 
                                               2.51/(reynolds*np.sqrt(f))))
        
        if reynolds < 2300:
            return 64/reynolds
        else:
            # Initial guess using Swamee-Jain equation
            f_0 = 0.25/(np.log10(self.roughness/(3.7*self.diameter*1000) + 5.74/reynolds**0.9)**2)
            return fsolve(colebrook, f_0)[0]
    
    def pressure_drop(self, velocity):
        """Calculate pressure drop using Darcy-Weisbach equation"""
        re = self.reynolds_number(velocity)
        f = self.friction_factor(re)
        return (f * self.length * self.density * velocity**2) / (2 * self.diameter)
    
    def velocity_profile(self, flow_rate, r_points=50):
        """Calculate velocity profile for laminar flow"""
        radius = self.diameter/2
        r = np.linspace(0, radius, r_points)
        
        # Maximum velocity at center
        v_max = 2 * flow_rate / (np.pi * radius**2)
        
        # Parabolic profile
        v = v_max * (1 - (r/radius)**2)
        return r, v
    
    def analyze_flow_range(self, velocities):
        """Analyze flow characteristics over a range of velocities"""
        reynolds = [self.reynolds_number(v) for v in velocities]
        pressure_drops = [self.pressure_drop(v) for v in velocities]
        friction_factors = [self.friction_factor(re) for re in reynolds]
        
        return reynolds, pressure_drops, friction_factors
    
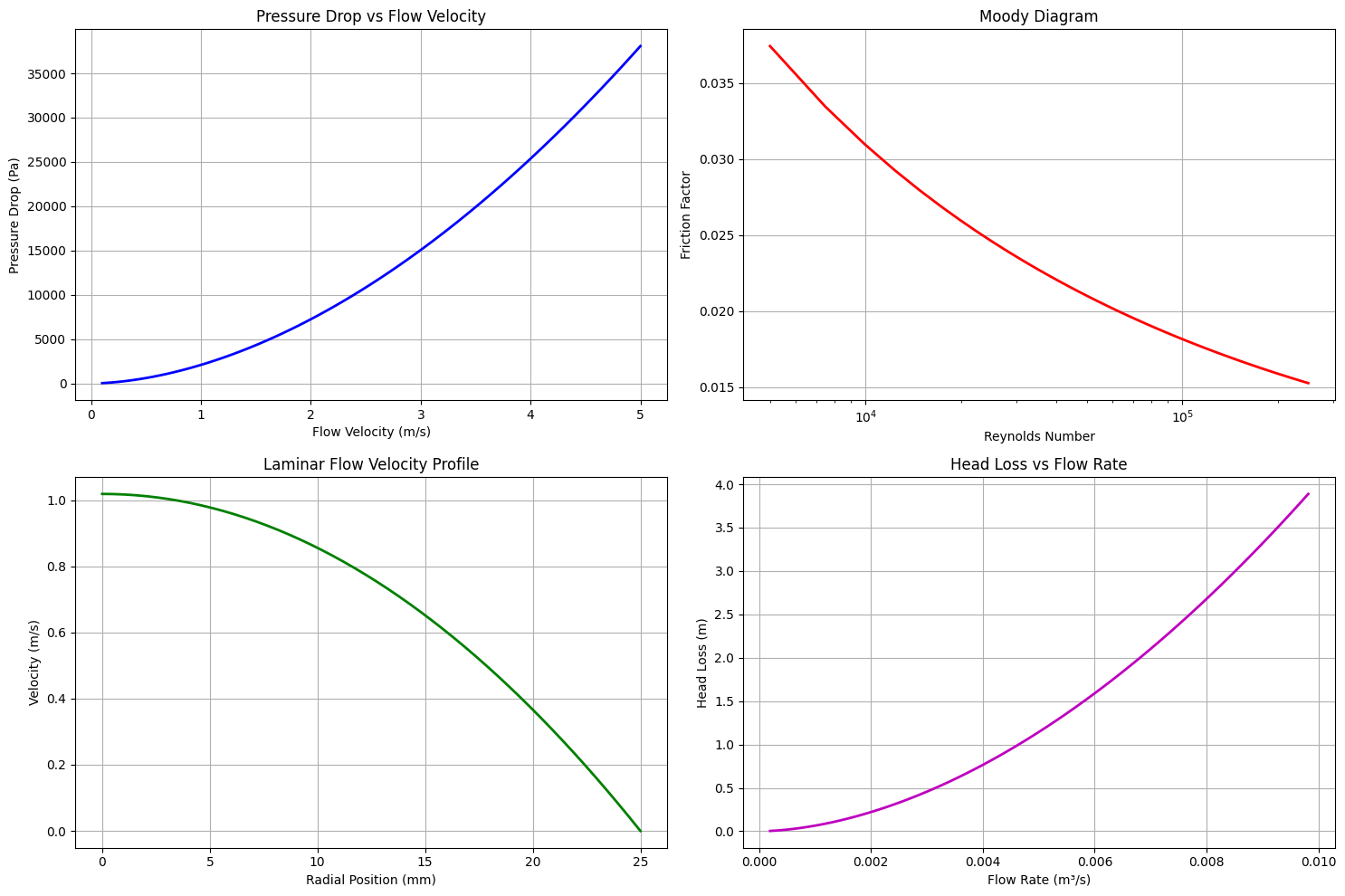
    def plot_analysis(self, velocities):
        """Create visualizations of flow analysis"""
        reynolds, pressure_drops, friction_factors = self.analyze_flow_range(velocities)
        
        fig = plt.figure(figsize=(15, 10))
        
        # Pressure drop vs Velocity
        ax1 = fig.add_subplot(221)
        ax1.plot(velocities, pressure_drops, 'b-', linewidth=2)
        ax1.set_xlabel('Flow Velocity (m/s)')
        ax1.set_ylabel('Pressure Drop (Pa)')
        ax1.set_title('Pressure Drop vs Flow Velocity')
        ax1.grid(True)
        
        # Friction factor vs Reynolds number
        ax2 = fig.add_subplot(222)
        ax2.semilogx(reynolds, friction_factors, 'r-', linewidth=2)
        ax2.set_xlabel('Reynolds Number')
        ax2.set_ylabel('Friction Factor')
        ax2.set_title('Moody Diagram')
        ax2.grid(True)
        
        # Velocity profile for laminar flow
        ax3 = fig.add_subplot(223)
        flow_rate = 0.001  # m³/s
        r, v = self.velocity_profile(flow_rate)
        ax3.plot(r*1000, v, 'g-', linewidth=2)  # Convert radius to mm
        ax3.set_xlabel('Radial Position (mm)')
        ax3.set_ylabel('Velocity (m/s)')
        ax3.set_title('Laminar Flow Velocity Profile')
        ax3.grid(True)
        
        # Head loss vs Flow rate
        ax4 = fig.add_subplot(224)
        head_losses = [dp/(self.density * 9.81) for dp in pressure_drops]
        flow_rates = [v * np.pi * (self.diameter/2)**2 for v in velocities]
        ax4.plot(flow_rates, head_losses, 'm-', linewidth=2)
        ax4.set_xlabel('Flow Rate (m³/s)')
        ax4.set_ylabel('Head Loss (m)')
        ax4.set_title('Head Loss vs Flow Rate')
        ax4.grid(True)
        
        plt.tight_layout()
        return fig

# Create analyzer and run analysis
analyzer = PipeFlowAnalyzer()

# Define velocity range for analysis
velocities = np.linspace(0.1, 5, 100)

# Plot results
analyzer.plot_analysis(velocities)

# Print analysis for specific velocity
test_velocity = 1.0  # m/s
re = analyzer.reynolds_number(test_velocity)
dp = analyzer.pressure_drop(test_velocity)
f = analyzer.friction_factor(re)

print("Pipe Flow Analysis Results:")
print(f"\nTest conditions at velocity = {test_velocity} m/s:")
print(f"Reynolds Number: {re:.0f}")
print(f"Flow Regime: {'Laminar' if re < 2300 else 'Turbulent'}")
print(f"Friction Factor: {f:.4f}")
print(f"Pressure Drop: {dp/1000:.2f} kPa")
print(f"Head Loss: {dp/(analyzer.density * 9.81):.2f} m")

Let me explain this pipe flow analysis example:

  1. Core Fluid Dynamics Concepts:

    • $Hagen$-$Poiseuille$ flow
    • Reynolds number
    • Friction factor
    • Pressure drop
    • Head loss

  2. Mathematical Components:

    • $Darcy$-$Weisbach$ equation
    • $Colebrook$-$White$ equation
    • Velocity profile calculations
    • Head loss computations

  3. Visualization Elements:

    • Top left: Pressure drop vs. flow velocity
    • Top right: Moody diagram (friction factor vs. Reynolds number)
    • Bottom left: Velocity profile in pipe
    • Bottom right: Head loss vs. flow rate

  4. Key Analysis Features:

    • Flow regime determination
    • Friction factor calculation
    • Pressure loss prediction
    • Velocity distribution

  5. Engineering Applications:

    • Pipe system design
    • Pump selection
    • Energy loss calculations
    • Flow rate optimization

Output

Pipe Flow Analysis Results:

Test conditions at velocity = 1.0 m/s:
Reynolds Number: 49910
Flow Regime: Turbulent
Friction Factor: 0.0210
Pressure Drop: 2.10 kPa
Head Loss: 0.21 m

The visualizations help understand:

  • How pressure drop varies with flow velocity
  • The relationship between friction factor and Reynolds number
  • The shape of the velocity profile in the pipe
  • Energy losses in pipe systems