Monetary Policy Simulation

We will simulate the effects of monetary policy on an economy using a simplified model.

The main variables are:

  1. Interest Rate (r):
    Set by the central bank.
  2. Inflation Rate (π):
    Determined by economic conditions and influenced by monetary policy.
  3. Output Gap (Y):
    The difference between actual output and potential output, affected by interest rate changes.

This simulation will follow the logic of the Taylor Rule, a common monetary policy guideline:
$$
r = r^* + \phi_\pi (\pi - \pi^*) + \phi_Y Y
$$

  • $(r^*)$ is the neutral interest rate.
  • $(\pi^*)$ is the target inflation rate.
  • $(\phi_\pi) and (\phi_Y)$ are policy reaction coefficients for inflation and output gap.

Python Implementation

Below is the $Python$ code to simulate the impact of monetary policy adjustments on inflation and the output gap over time.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
import numpy as np
import matplotlib.pyplot as plt

# Parameters for the model
r_star = 2.0  # Neutral interest rate (% per year)
pi_star = 2.0  # Target inflation rate (% per year)
phi_pi = 1.5   # Reaction to inflation deviation
phi_Y = 0.5    # Reaction to output gap

# Initial conditions
T = 20  # Number of periods
time = np.arange(1, T + 1)

# Arrays to store values
inflation = np.zeros(T)
output_gap = np.zeros(T)
interest_rate = np.zeros(T)

# Initial values
inflation[0] = 3.0  # Initial inflation rate
output_gap[0] = -1.0  # Initial output gap

# Simulation loop
for t in range(1, T):
    # Determine interest rate using the Taylor Rule
    interest_rate[t] = (
        r_star + phi_pi * (inflation[t-1] - pi_star) + phi_Y * output_gap[t-1]
    )
    
    # Update output gap and inflation based on interest rate
    output_gap[t] = output_gap[t-1] - 0.5 * (interest_rate[t] - r_star)
    inflation[t] = inflation[t-1] - 0.3 * output_gap[t]

# Plotting the results
plt.figure(figsize=(12, 8))

# Plot inflation
plt.subplot(3, 1, 1)
plt.plot(time, inflation, label='Inflation Rate', color='red')
plt.axhline(pi_star, linestyle='--', color='black', label='Target Inflation Rate')
plt.title('Monetary Policy Simulation')
plt.ylabel('Inflation Rate (%)')
plt.legend()

# Plot output gap
plt.subplot(3, 1, 2)
plt.plot(time, output_gap, label='Output Gap', color='blue')
plt.axhline(0, linestyle='--', color='black', label='Zero Output Gap')
plt.ylabel('Output Gap (%)')
plt.legend()

# Plot interest rate
plt.subplot(3, 1, 3)
plt.plot(time, interest_rate, label='Interest Rate', color='green')
plt.axhline(r_star, linestyle='--', color='black', label='Neutral Interest Rate')
plt.xlabel('Time (Periods)')
plt.ylabel('Interest Rate (%)')
plt.legend()

plt.tight_layout()
plt.show()

Explanation of the Code

  1. Model Setup:
    • The neutral interest rate $(r^*)$, target inflation rate $(\pi^*)$, and policy reaction coefficients $(\phi_\pi$, $\phi_Y)$ are defined.
  2. Simulation Loop:
    • The interest rate is updated using the Taylor Rule.
    • The output gap and inflation rate are updated based on the interest rate, reflecting the dynamics of monetary policy.
  3. Visualization:
    • The results for inflation, output gap, and interest rate over time are plotted.

Expected Results

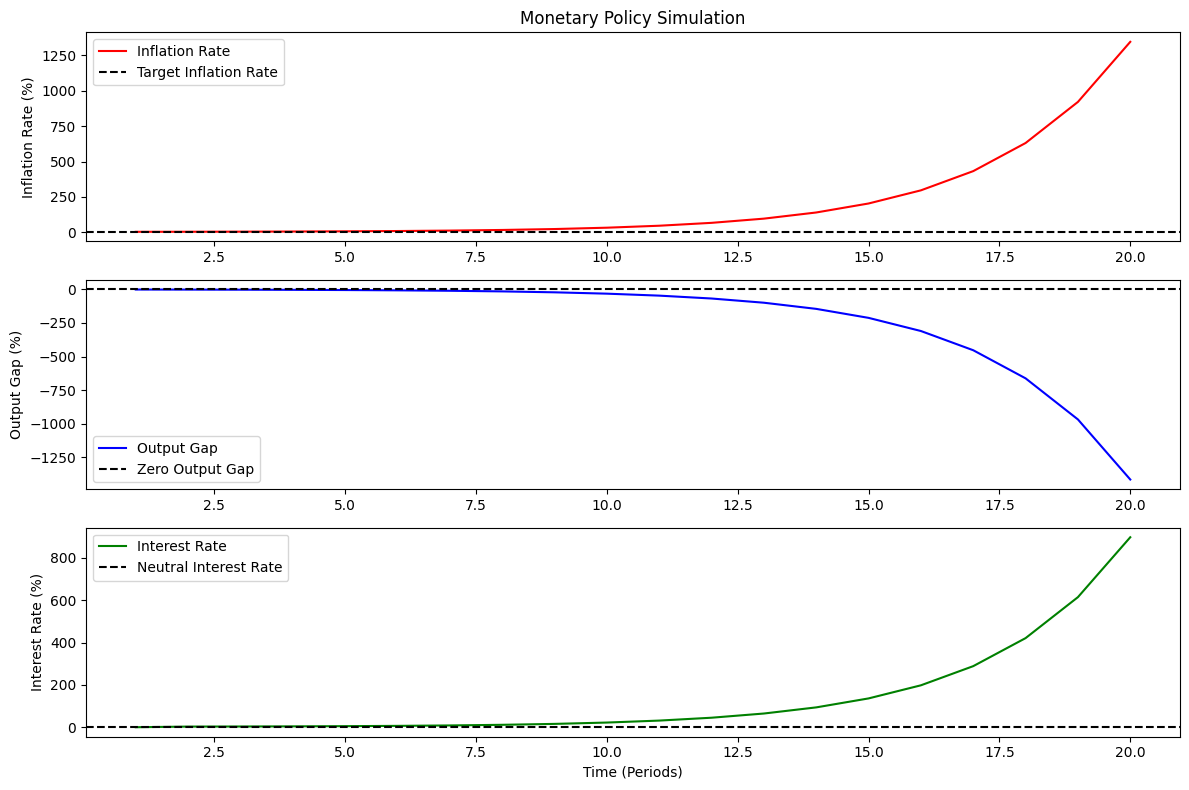
  1. Inflation Rate:
    Gradually converges toward the target rate $(\pi^* = 2％)$.
  2. Output Gap:
    Oscillates and eventually stabilizes around zero.
  3. Interest Rate:
    Adjusts dynamically based on the Taylor Rule to stabilize inflation and output.

The graphs will visually illustrate these dynamics, helping to understand how monetary policy impacts an economy over time.