微分方程式の数値解法 SciPy

微分方程式の数値解法

SciPyを使って、偏微分方程式の数値解法を行います。

偏微分方程式の解法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
import numpy as np
from scipy.integrate import solve_bvp
import matplotlib.pyplot as plt

# 微分方程式と境界条件の定義
def fun(x, y):
    return np.vstack((y[1], -np.exp(y[0])))

def bc(ya, yb):
    return np.array([ya[0] - 1, yb[0] - 2])

# メッシュ生成
x = np.linspace(0, 1, 5)
y = np.zeros((2, x.size))

# 微分方程式の解法
sol = solve_bvp(fun, bc, x, y)

# 結果のプロット
x_plot = np.linspace(0, 1, 100)
y_plot = sol.sol(x_plot)[0]

plt.plot(x_plot, y_plot, label='solution')
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.title('Solution of BVP')
plt.grid()
plt.show()

[実行結果]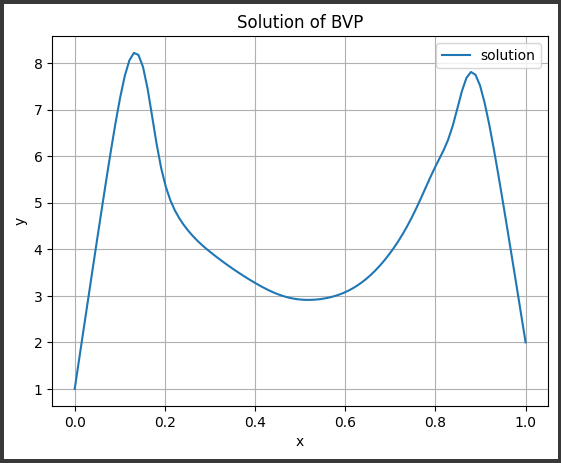

ソースコード解説

このソースコードは、境界値問題 (Boundary Value Problem, BVP) を解くためのものです。

コードの各部分を詳しく説明します。

1. ライブラリのインポート

1
2
3
import numpy as np
from scipy.integrate import solve_bvp
import matplotlib.pyplot as plt
  • numpy (np): 数値計算用のライブラリで、配列操作や数学関数を提供します。
  • solve_bvp: SciPyライブラリの関数で、境界値問題を解くために使用します。
  • matplotlib.pyplot (plt): グラフ描画用のライブラリです。

2. 微分方程式と境界条件の定義

1
2
3
4
5
def fun(x, y):
    return np.vstack((y[1], -np.exp(y[0])))

def bc(ya, yb):
    return np.array([ya[0] - 1, yb[0] - 2])
  • fun(x, y): 微分方程式を定義する関数です。
    ここでは、連立一次微分方程式の形式で表されています。
    • y[0] は$ ( y ) $を表し、y[1] は$ ( y’ ) $を表します。
    • np.vstack((y[1], -np.exp(y[0]))) は、微分方程式の右辺をベクトル形式で返します。
  • bc(ya, yb): 境界条件を定義する関数です。
    • ya[0] - 1 は$ ( x = 0 ) $での境界条件を表し、yb[0] - 2 は$ ( x = 1 ) $での境界条件を表します。

3. メッシュ生成

1
2
x = np.linspace(0, 1, 5)
y = np.zeros((2, x.size))
  • np.linspace(0, 1, 5): $( x ) $の値を$ [0, 1] $の範囲で等間隔に$5$点生成します。
  • np.zeros((2, x.size)): $( y ) $の初期推定値をゼロで初期化します。
    ここでは$ ( y ) $と$ ( y’ ) $の初期値を与えています。

4. 微分方程式の解法

1
sol = solve_bvp(fun, bc, x, y)
  • solve_bvp(fun, bc, x, y): 定義した微分方程式と境界条件を解きます。
    • fun: 微分方程式の関数。
    • bc: 境界条件の関数。
    • x: メッシュ点。
    • y: 初期推定値。

5. 結果のプロット

1
2
3
4
5
6
7
8
9
10
x_plot = np.linspace(0, 1, 100)
y_plot = sol.sol(x_plot)[0]

plt.plot(x_plot, y_plot, label='solution')
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.title('Solution of BVP')
plt.grid()
plt.show()
  • np.linspace(0, 1, 100): 解を詳細にプロットするために、$[0, 1] $の範囲で$100$点のメッシュを生成します。
  • sol.sol(x_plot)[0]: 解を評価し、プロット用の$ ( y ) $の値を取得します。
  • plt.plot(x_plot, y_plot, label='solution'): 解のプロットを作成します。
  • plt.xlabel('x'): $x$軸のラベルを設定します。
  • plt.ylabel('y'): $y$軸のラベルを設定します。
  • plt.legend(): 凡例を追加します。
  • plt.title('Solution of BVP'): グラフのタイトルを設定します。
  • plt.grid(): グリッド線を追加します。
  • plt.show(): グラフを表示します。

このコードは、境界値問題の解を求め、その解をプロットするプロセスを示しています。

具体的には、非線形微分方程式 $( y’’ = -\exp(y) ) $を境界条件 $ ( y(0) = 1 ) $および$ ( y(1) = 2 ) $の下で解き、その結果をグラフで表示しています。

結果解説

[実行結果]

このグラフは境界値問題 (Boundary Value Problem, BVP) の解を示しています。

グラフの説明

  • タイトル: “Solution of BVP”

    • 境界値問題の解を示すグラフであることがわかります。

  • x軸: $x$

    • 自変数 $ (x) $の値を示しています。範囲は$ 0 $から$ 1 $までです。

  • y軸: $y$

    • 従変数 $ (y) $の値を示しています。これは BVP の解の値です。

  • プロット: 青い線

    • 境界値問題の解の値が$ (x) $に対してどのように変化するかを示しています。

境界値問題の概要

境界値問題は、微分方程式の解が特定の境界条件を満たすように求められる問題です。

このグラフは、与えられた境界条件のもとで得られた微分方程式の解をプロットしています。

  • 解の特徴:
    • $(x)$ が $0$ のとき、$(y) $の値は約$ 1$。
    • $(x)$ が $0.2$ 付近でピークが見られ、最大値は約$ 8$。
    • $(x)$ が $0.8$ 付近で別のピークが見られ、再度最大値は約$ 8$。
    • $(x)$ が $1$ のとき、再び$ (y) $の値は約$ 1 $まで減少しています。

このような形状は、境界条件と微分方程式の特性から生じるものです。

具体的な境界条件や微分方程式の形式によって異なる解が得られるため、このグラフは特定の条件下での一例を示しています。