3Dグラフ

3Dグラフ

以下の方程式を使用して3Dグラフを描いてみます：

$$
z = \frac{\sin(x^2 + y^2)}{x^2 + y^2}
$$

この方程式は、中心が原点で放射状に渦巻くような形を描くことが知られています。

これをMatplotlibを用いて描画してみましょう。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import numpy as np

# データの生成
x = np.linspace(-5, 5, 100)
y = np.linspace(-5, 5, 100)
x, y = np.meshgrid(x, y)
z = np.sin(x**2 + y**2) / (x**2 + y**2)

# プロット
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(x, y, z, cmap='viridis')

# ラベルとタイトルの設定
ax.set_xlabel('X Label')
ax.set_ylabel('Y Label')
ax.set_zlabel('Z Label')
ax.set_title('3D Plot of $z = \\frac{\\sin(x^2 + y^2)}{x^2 + y^2}$')

plt.show()

このコードでは、$ ( z = \frac{\sin(x^2 + y^2)}{x^2 + y^2} ) $の関数を使用して、$x$と$y$の範囲で$z$を計算し、それを3D表面プロットとして描画しています。

Matplotlibの plot_surface メソッドで表面を描画し、軸ラベルとタイトルも設定しています。

このグラフでは、原点を中心にして放射状に波打つ特徴的な形状が描かれることが期待されます。

[実行結果]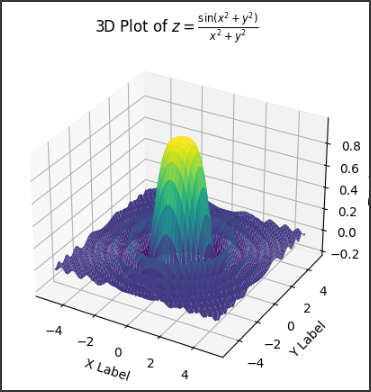

他にもさまざまな数学的な関数や方程式を試して、興味深い3Dグラフを作成してみてください。

ソースコード解説

ソースコードの説明をします。

1. ライブラリのインポート

1
2
3
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import numpy as np
  • matplotlib.pyplot: Matplotlibのプロット機能を利用するためのモジュール。
    pltとしてインポートされています。
  • mpl_toolkits.mplot3d.Axes3D: 3次元のプロットを扱うためのクラスが含まれています。
  • numpy: 数値計算を行うための基本的なモジュール。
    npとしてインポートされています。

2. データの生成

1
2
3
4
x = np.linspace(-5, 5, 100)
y = np.linspace(-5, 5, 100)
x, y = np.meshgrid(x, y)
z = np.sin(x**2 + y**2) / (x**2 + y**2)
  • np.linspace(-5, 5, 100): $-5$から$5$までの範囲を等間隔に区切った$100$個の数値を生成し、それらが$x$および$y$の値として使用されます。
  • np.meshgrid(x, y): xとyの配列から格子状の座標を生成します。
    これにより、$x$と$y$の組み合わせがすべて生成され、それに対応する$z$値が計算されます。
  • z = np.sin(x**2 + y**2) / (x**2 + y**2): 指定された数学的な関数を使用して$z$値を計算します。
    ここでは$ ( z = \frac{\sin(x^2 + y^2)}{x^2 + y^2} ) $を計算しています。

3. プロットの設定と描画

1
2
3
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(x, y, z, cmap='viridis')
  • plt.figure(): 新しい図を生成します。
  • fig.add_subplot(111, projection='3d'): 3D描画用のサブプロットを設定します。
    ここで111は1行1列の1番目の位置を意味し、projection='3d'で3D描画を有効にします。
  • ax.plot_surface(x, y, z, cmap='viridis'): $x$, $y$, $z$の値を使用して3D表面を描画します。
    cmap='viridis'はカラーマップを指定しています。

4. ラベルとタイトルの設定

1
2
3
4
ax.set_xlabel('X Label')
ax.set_ylabel('Y Label')
ax.set_zlabel('Z Label')
ax.set_title('3D Plot of $z = \\frac{\\sin(x^2 + y^2)}{x^2 + y^2}$')
  • ax.set_xlabel('X Label'), ax.set_ylabel('Y Label'), ax.set_zlabel('Z Label'): $x$軸、$y$軸、$z$軸のラベルを設定します。
  • ax.set_title('3D Plot of $z = \\frac{\\sin(x^2 + y^2)}{x^2 + y^2}$'): プロットのタイトルを設定します。
    ここではLaTeXの数式を用いてzの式をタイトルに表示しています。

5. プロットの表示

1
plt.show()
  • plt.show(): 最後にプロットを表示します。

このようにして、与えられた数学的な関数を基にして、3Dの表面プロットをMatplotlibを使って作成することができます。