チェビシェフ多項式（Chebyshev polynomials

チェビシェフ多項式（Chebyshev polynomials

チェビシェフ多項式（Chebyshev polynomials）は、直交多項式の一種であり、特に数値解析や近似理論で広く使用されています。

チェビシェフ多項式は第一種と第二種があり、ここでは第一種のチェビシェフ多項式$ ( T_n(x) ) $を Python でプロットしてみます。

第一種のチェビシェフ多項式$ ( T_n(x) ) $は次の漸化式で定義されます：
$$
[ T_0(x) = 1 ]
$$
$$
[ T_1(x) = x ]
$$
$$
[ T_{n+1}(x) = 2xT_n(x) - T_{n-1}(x) ]
$$

Python でチェビシェフ多項式を計算し、グラフ化するために numpy と matplotlib ライブラリを使用します。

以下に、チェビシェフ多項式をプロットするコードを示します。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
import numpy as np
import matplotlib.pyplot as plt

# チェビシェフ多項式を計算する関数
def chebyshev_polynomials(n, x):
    if n == 0:
        return np.ones_like(x)
    elif n == 1:
        return x
    else:
        T0 = np.ones_like(x)
        T1 = x
        for _ in range(2, n + 1):
            T2 = 2 * x * T1 - T0
            T0, T1 = T1, T2
        return T1

# x の範囲を定義
x = np.linspace(-1, 1, 400)

# プロットするチェビシェフ多項式の次数
degrees = [0, 1, 2, 3, 4, 5]

# グラフの作成
plt.figure(figsize=(10, 6))

for degree in degrees:
    Tn = chebyshev_polynomials(degree, x)
    plt.plot(x, Tn, label=f'T_{degree}(x)')

# グラフの装飾
plt.title('Chebyshev Polynomials of the First Kind')
plt.xlabel('x')
plt.ylabel('T_n(x)')
plt.legend()
plt.grid(True)
plt.axhline(0, color='black',linewidth=0.5)
plt.axvline(0, color='black',linewidth=0.5)
plt.show()

このコードは、チェビシェフ多項式を計算し、それらをグラフにプロットします。

chebyshev_polynomials 関数は、指定した次数のチェビシェフ多項式を計算します。

x の範囲を$ -1 $から$ 1 $に設定し、次数$ 0 $から$ 5 $までのチェビシェフ多項式をプロットしています。

このスクリプトを実行すると、チェビシェフ多項式のグラフが表示されます。

それぞれの多項式の形状を観察することで、チェビシェフ多項式の特性を理解する助けになります。

[実行結果]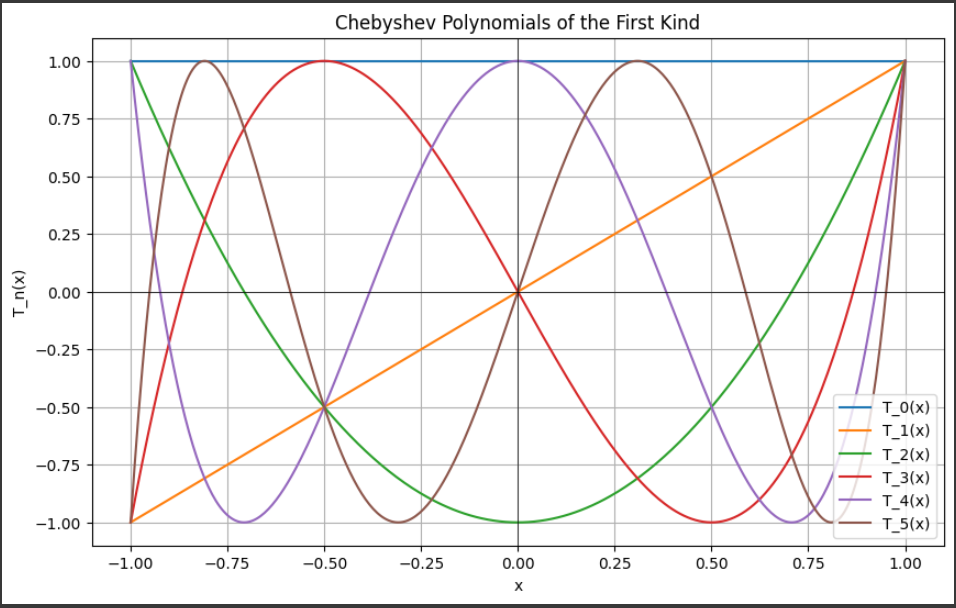

ソースコード解説

このソースコードは、Python を使って第一種のチェビシェフ多項式を計算し、プロットするためのものです。
ソースコードを詳しく説明します。

1. ライブラリのインポート

1
2
import numpy as np
import matplotlib.pyplot as plt

まず、必要なライブラリをインポートします。

  • numpy (np): 数値計算を効率的に行うためのライブラリです。
    ここではチェビシェフ多項式の計算や範囲の設定に使用します。
  • matplotlib.pyplot (plt): データを可視化するためのライブラリです。
    ここではグラフの描画に使用します。

2. チェビシェフ多項式を計算する関数

1
2
3
4
5
6
7
8
9
10
11
12
def chebyshev_polynomials(n, x):
    if n == 0:
        return np.ones_like(x)
    elif n == 1:
        return x
    else:
        T0 = np.ones_like(x)
        T1 = x
        for _ in range(2, n + 1):
            T2 = 2 * x * T1 - T0
            T0, T1 = T1, T2
        return T1

この関数 chebyshev_polynomials(n, x) は、第一種のチェビシェフ多項式 $ ( T_n(x) ) $を計算します。

  • n: 多項式の次数です。
  • x: 多項式の計算に使用する x の値の配列です。

関数の中では、チェビシェフ多項式の定義に基づいて多項式を計算します。

  • $( T_0(x) = 1 )$:
    もし$ n $が$ 0 $ならば、$x $と同じ形状の全ての要素が$ 1 $の配列を返します。
  • $( T_1(x) = x )$:
    もし$ n $が$ 1 $ならば、$x $をそのまま返します。
  • $( T_{n+1}(x) = 2xT_n(x) - T_{n-1}(x) )$:
    それ以外の場合は、漸化式を用いて高次の多項式を計算します。

3. x の範囲を定義

1
x = np.linspace(-1, 1, 400)

ここでは、$x $の範囲を$ -1 $から$ 1 $までの$ 400 $個の点で定義しています。
np.linspace は指定した範囲内で均等に分布する数値を生成する関数です。

4. プロットするチェビシェフ多項式の次数

1
degrees = [0, 1, 2, 3, 4, 5]

プロットするチェビシェフ多項式の次数をリストで定義しています。
ここでは$ 0 $から$ 5 $までの多項式をプロットします。

5. グラフの作成

1
plt.figure(figsize=(10, 6))

新しい図（figure）を作成し、そのサイズを 10x6 インチに設定します。
これにより、グラフの全体的な見栄えを調整します。

6. チェビシェフ多項式の計算とプロット

1
2
3
for degree in degrees:
    Tn = chebyshev_polynomials(degree, x)
    plt.plot(x, Tn, label=f'T_{degree}(x)')

ここでは、指定された各次数のチェビシェフ多項式を計算し、プロットします。

  • for degree in degrees:
    各次数に対して繰り返し処理を行います。
  • Tn = chebyshev_polynomials(degree, x):
    現在の次数のチェビシェフ多項式を計算します。
  • plt.plot(x, Tn, label=f'T_{degree}(x)'):
    計算した多項式をプロットし、凡例にその次数をラベル付けします。

7. グラフの装飾

1
2
3
4
5
6
7
8
plt.title('Chebyshev Polynomials of the First Kind')
plt.xlabel('x')
plt.ylabel('T_n(x)')
plt.legend()
plt.grid(True)
plt.axhline(0, color='black',linewidth=0.5)
plt.axvline(0, color='black',linewidth=0.5)
plt.show()

最後に、グラフに装飾を加えます。

  • plt.title('Chebyshev Polynomials of the First Kind'): グラフにタイトルを追加します。
  • plt.xlabel('x'): $x$軸にラベルを追加します。
  • plt.ylabel('T_n(x)'): $y$軸にラベルを追加します。
  • plt.legend(): 凡例を表示します。
  • plt.grid(True): グリッド線を表示します。
  • plt.axhline(0, color='black', linewidth=0.5): $y=0 $の水平線を追加します。
  • plt.axvline(0, color='black', linewidth=0.5): $x=0 $の垂直線を追加します。
  • plt.show(): グラフを表示します。

このコード全体を通して、第一種のチェビシェフ多項式 $ ( T_n(x) ) $の異なる次数のプロットを生成し、可視化することができます。

それぞれの多項式の形状を観察することで、チェビシェフ多項式の特性を理解することができます。

グラフ解説

[実行結果]

このグラフには、第一種のチェビシェフ多項式 $ ( T_n(x) ) $が表示されます。

グラフの詳細な内容について説明します。

グラフの詳細

1. タイトル:

グラフのタイトルには “Chebyshev Polynomials of the First Kind” と表示されています。
これは、第一種のチェビシェフ多項式を示しています。

2. x軸:

$x$軸は$ -1 $から$ 1 $の範囲を持ちます。
これは、チェビシェフ多項式が$ -1 $から$ 1 $の範囲で特に重要な特性を持つためです。

3. y軸:

$y$軸は、多項式の値を表します。
異なる次数のチェビシェフ多項式の値がこの軸にプロットされます。

4. プロットされる多項式:

グラフには、次数$ 0 $から$ 5 $までのチェビシェフ多項式がプロットされています。
それぞれの多項式は異なる色で表示され、凡例により識別できます。

  • $( T_0(x) )$:
    $( T_0(x) = 1 ) $なので、$x $に関係なく$ y $値が常に $1$ です。
    これは$ y = 1 $の水平線として表示されます。
  • $( T_1(x) )$:
    $( T_1(x) = x ) $なので、$y = x $の直線として表示されます。
    原点を通る斜めの直線です。
  • $( T_2(x) )$:
    $( T_2(x) = 2x^2 - 1 ) $で、放物線の形をしています。
    $x $が$ -1 $または$ 1 $のときに$ y $が$ 1 $になり、$x $が$ 0 $のときに $y $が $-1 $になります。
  • $( T_3(x) )$:
    $( T_3(x) = 4x^3 - 3x ) $で、三次多項式の形をしています。
    $x $の正負に応じて $y $の値が変化し、波のような形をしています。
  • $( T_4(x) )$:
    $( T_4(x) = 8x^4 - 8x^2 + 1 ) $で、四次多項式の形をしています。
    2つの波があるように見えます。
  • $( T_5(x) )$:
    $( T_5(x) = 16x^5 - 20x^3 + 5x ) $で、五次多項式の形をしています。
    より複雑な波形になります。

5. 凡例:

グラフの右上に凡例があり、それぞれの曲線がどの次数のチェビシェフ多項式であるかを示しています。
例えば、$T_0(x)$ や $T_1(x)$ などのラベルが表示されています。

6. グリッド線:

グラフにはグリッド線が表示されており、プロットされた多項式の値を読み取りやすくしています。

7. 軸線:

$x$軸と $y$軸の交点に黒い線が引かれています。
これは、原点を明確に示し、多項式が$ x $軸や$ y $軸と交差する点を見つけやすくしています。

具体的な観察点

  • 対称性:
    $ ( T_n(x) ) $のうち偶数の多項式は偶関数（対称性が$ x $軸に対して対称）であり、奇数の多項式は奇関数（対称性が原点に対して対称）です。
    例えば、 $( T_2(x) ) $は偶関数であり、 $( T_3(x) ) $は奇関数です。

  • 振動の数:
    $ ( T_n(x) ) $は$ -1 $から$ 1 $の間で$ ( n ) $回振動します。
    例えば、$ ( T_3(x) ) $は$ -1$ から$ 1 $の間で$ 3 $回振動します。

  • 極値:
    チェビシェフ多項式の極値の位置と値は、数値解析や近似理論において重要です。
    例えば、$ ( T_2(x) ) $の極値は$ ( x = \pm 1/\sqrt{2} ) $にあり、それぞれ$ y = -1 $です。

このように、チェビシェフ多項式のグラフを観察することで、彼らの特性や挙動を理解しやすくなります。