ボーアの周期律

ボーアの周期律

ボーアの周期律は、ボーアの原子模型に基づいて、原子の電子配置と元素の性質の周期的変化を説明する法則です。

主な内容は以下の通りです。

  1. 電子は特定の軌道上を回っており、その軌道半径と運動エネルギーは主量子数$n$によって決まる。

  2. 電子は各軌道に$2n^2$個まで収容できる。
    $n=1$のK殻には$2$電子、$n=2$のL殻には$8$電子が入る。

  3. 原子内の電子は最小のエネルギー準位から順に殻や軌道に入っていく。

  4. 同じ主量子数の軌道では、エネルギー準位が低い順に$ s$, $p$, $d$, $f$ と入っていく。

  5. 原子番号が増えるにつれ、電子配置が規則的に変化する。
    同じ電子配置を持つ元素は、化学的性質が似通っている。

  6. 各周期では、アルカリ金属からハロゲンまで電子配置が変化し、性質も周期的に変化する。

  7. 同じ族の元素は外側電子の数が同じなので、化学的性質が似ている。

このように、ボーアの周期律は電子配置に基づいて元素の性質を周期的に整理し、周期表の作成につながりました。

しかし完全ではなく、後にさらに発展した量子力学的な考え方に置き換えられています。

ソースコード

ボーアの原子模型に基づく原子のエネルギー準位は、次の式で与えられます：

$$
E_n = -\frac{k \cdot Z^2 \cdot R_H}{n^2}
$$

ここで、$(E_n) $は第$ (n) $準位のエネルギー、$(k) $はクーロン定数、$(Z) $は原子番号、$(R_H) $はリュードベリ定数、$(n) $は主量子数です。

Pythonを使用してこの式を解き、結果をグラフ化する例を以下に示します。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
import numpy as np
import matplotlib.pyplot as plt

def bohr_energy(n, Z=1):
    k = 8.9875517923e9  # クーロン定数 [N m^2 / C^2]
    R_H = 2.1798741e-18  # リュードベリ定数 [J]
    return -(k * Z**2 * R_H) / n**2

# 原子番号
Z = 1  # 水素原子の場合

# 主量子数の範囲を定義
n_values = np.arange(1, 11)

# エネルギー準位を計算
energy_levels = [bohr_energy(n, Z) for n in n_values]

# グラフをプロット
plt.figure(figsize=(8, 6))
plt.plot(n_values, energy_levels, marker='o', linestyle='-')
plt.title('Bohr Model Energy Levels')
plt.xlabel('Principal Quantum Number (n)')
plt.ylabel('Energy (J)')
plt.grid(True)
plt.show()

このコードでは、主量子数$ (n) $ の値に対するエネルギー準位を計算し、それをグラフ化しています。

[実行結果]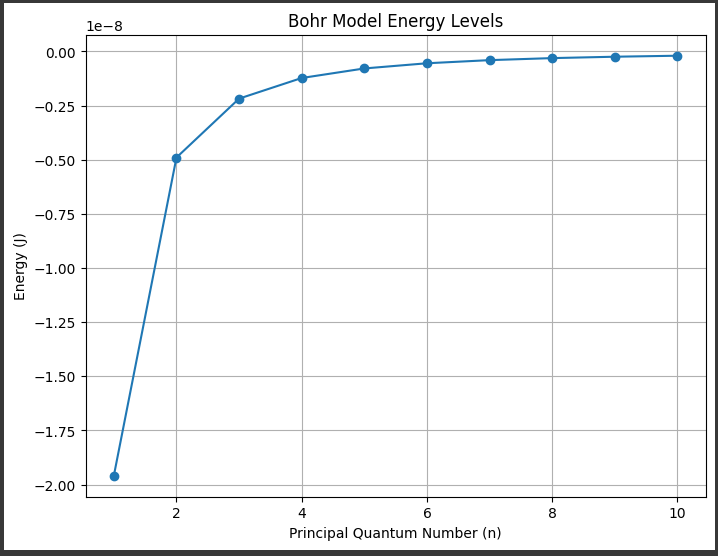

ソースコード解説

ソースコードの各部分を説明します。

1. NumPyとMatplotlibのインポート:

1
2
import numpy as np
import matplotlib.pyplot as plt
  • NumPyはPythonで数値計算を行うためのライブラリです。
  • MatplotlibはPythonでグラフ描画を行うためのライブラリです。
    このスクリプトでは、Matplotlibのpyplotモジュールを使用しています。

2. ボーアのエネルギー計算関数:

1
2
3
4
def bohr_energy(n, Z=1):
   k = 8.9875517923e9  # クーロン定数 [N m^2 / C^2]
   R_H = 2.1798741e-18  # リュードベリ定数 [J]
   return -(k * Z**2 * R_H) / n**2
  • bohr_energy 関数は、ボーアの原子模型に基づいて与えられた主量子数$ (n) $に対する原子のエネルギー準位を計算します。
    デフォルトでは水素原子の場合を考慮しており、原子番号$ (Z) $が$1$となっています。

3. 原子番号の設定:

1
Z = 1  # 水素原子の場合
  • Z は原子の原子番号を表し、ここでは水素原子の場合を考慮しています。

4. 主量子数の範囲の定義:

1
n_values = np.arange(1, 11)
  • np.arange 関数を使って、主量子数$ (n) $の値を$1$から$10$までの範囲で定義しています。

5. エネルギー準位の計算:

1
energy_levels = [bohr_energy(n, Z) for n in n_values]
  • bohr_energy 関数を使って、与えられた主量子数$ (n) $に対するエネルギー準位を計算し、リスト energy_levels に格納しています。

6. グラフのプロット:

1
2
3
4
5
6
7
plt.figure(figsize=(8, 6))
plt.plot(n_values, energy_levels, marker='o', linestyle='-')
plt.title('Bohr Model Energy Levels')
plt.xlabel('Principal Quantum Number (n)')
plt.ylabel('Energy (J)')
plt.grid(True)
plt.show()
  • Matplotlibを使ってグラフを作成し、エネルギー準位を表示しています。
  • plt.figure(figsize=(8, 6)) でグラフのサイズを設定します。
  • plt.plot で n_values に対する energy_levels をプロットし、マーカー ‘o’ を使用してデータ点を示し、直線でデータ点をつなぎます。
  • グラフのタイトル、軸ラベルを設定し、グリッドを表示しています。
  • plt.show() でグラフを表示します。

結果解説

[実行結果]

このグラフは、ボーアの原子模型に基づいて計算された原子のエネルギー準位を示しています。

以下は、グラフに表示される内容の詳細な説明です。

1. x軸:

  • x軸は主量子数$ (n) $を表しています。
    主量子数は、電子が原子の中心から離れた軌道またはエネルギー準位を示します。
    主量子数が大きくなるにつれて、電子のエネルギー準位が上昇します。

2. y軸:

  • y軸はエネルギーを表しています。
    エネルギーはボーアの原子模型によって予測された値であり、主量子数$ (n) $に依存します。
    負の値を持つことに注意してください。
    これは、電子が原子核に束縛されているため、系全体のエネルギーが負の値となるためです。

3. グラフのプロット:

  • グラフには、主量子数$ (n) $に対するエネルギー準位がプロットされています。
    各点は、特定の主量子数$ (n) $に対応するエネルギーを示しています。
  • マーカー ‘o’ が使用されていますが、これはデータ点を示すための円を意味します。
  • 線はデータ点をつなぐための直線を表し、データの間の関係を視覚化します。

4. タイトル:

  • グラフのタイトルは “Bohr Model Energy Levels” となっており、ボーアの原子模型に基づくエネルギー準位を示していることを示しています。

5. 軸ラベル:

  • x軸は “Principal Quantum Number (n)” とラベル付けされており、主量子数$ (n) $を示します。
  • y軸は “Energy (J)” とラベル付けされており、エネルギーをジュール単位で示しています。

6. グリッド:

  • グラフには背景にグリッドが表示されており、データ点の位置を見やすくし、目盛り線に沿ってデータを読み取るのを助けます。

このグラフは、主量子数$ (n) $とエネルギーの関係を視覚化し、ボーアの原子模型に基づく原子のエネルギー準位の理解を支援します。