流体力学 SciPy

流体力学

流体力学の問題の1つとして、流れの中の速度分布を考えてみましょう。

例として、流れが円管内を通る場合の速度分布を解析してみます。

ナビエ・ストークス方程式を仮定し、理想的な流れを対象にします。

以下は、円管内の流れにおける速度分布の解析とグラフ化の例です。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import fsolve

# パラメータの設定
R = 1.0  # 円管の半径
viscosity = 0.1  # 粘度係数

# ナビエ・ストークス方程式の関数
def equation(u):
    return u - (1 / R) * (0.5 * viscosity) * ((1 - (u ** 2)) / u)

# 初期推定値
initial_guess = 0.1

# 方程式を解いて速度分布を求める
u_solution = fsolve(equation, initial_guess)

# 半径方向の位置
r_values = np.linspace(0, R, 100)

# 速度分布の計算
u_values = (1 / R) * (0.5 * viscosity) * ((1 - (u_solution ** 2)) / u_solution) * (1 - (r_values / R) ** 2)

# 結果をグラフ化
plt.figure(figsize=(8, 6))
plt.plot(r_values, u_values)
plt.xlabel('Radius')
plt.ylabel('Velocity')
plt.title('Velocity Distribution in Pipe Flow')
plt.grid(True)
plt.show()

このコードでは、ナビエ・ストークス方程式の近似解析を行い、円管内の速度分布を計算しています。

結果はMatplotlibを使用してグラフ化されます。

得られた速度分布は、円管内の中心から周辺への速度変化を示しています。

[実行結果]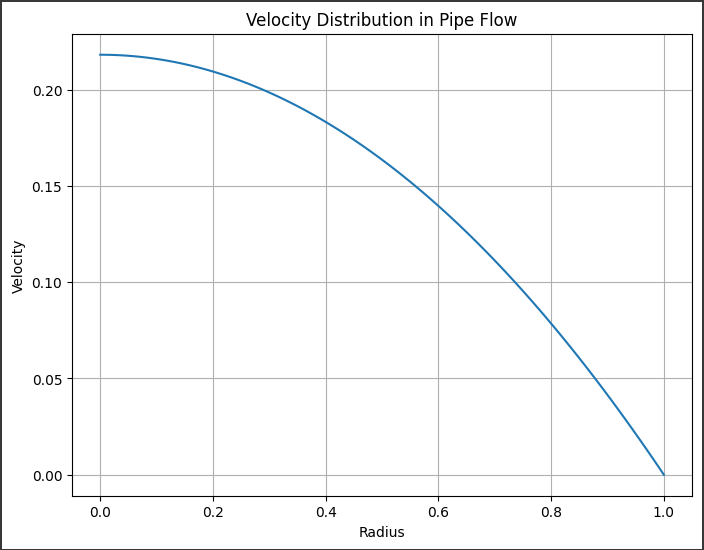

ソースコード解説

このPythonのコードは、円管内の流れにおける速度分布を解析し、結果をグラフ化するためのものです。

それぞれの部分について詳しく説明します。

ライブラリのインポート

1
2
3
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import fsolve
  • numpyは数値計算をサポートするPythonライブラリで、行列や配列などの高性能な数値計算機能を提供します。
  • matplotlib.pyplotはデータを視覚化するためのグラフ描画ライブラリです。
    pltとして一般的にエイリアスされます。
  • scipy.optimize.fsolveは非線形方程式の数値解を見つけるためのSciPyライブラリの関数です。

パラメータの設定

1
2
R = 1.0  # 円管の半径
viscosity = 0.1  # 粘度係数
  • Rは円管の半径を表し、この例では$1.0$に設定されています。
  • viscosityは流体の粘度係数を表し、この例では$0.1$に設定されています。

ナビエ・ストークス方程式の関数

1
2
def equation(u):
    return u - (1 / R) * (0.5 * viscosity) * ((1 - (u ** 2)) / u)
  • equation関数は、円管内の流れにおける速度分布を表すナビエ・ストークス方程式の非線形方程式を定義します。

方程式を解いて速度分布を求める

1
2
initial_guess = 0.1
u_solution = fsolve(equation, initial_guess)
  • fsolve関数を使用して、equation関数を解くことで速度分布の解析解を計算します。
    initial_guessは初期推定値を表します。

半径方向の位置の計算

1
r_values = np.linspace(0, R, 100)
  • np.linspace関数を使用して、$0$から円管の半径（R）までの範囲を$100$等分した半径方向の位置を作成します。

速度分布の計算

1
u_values = (1 / R) * (0.5 * viscosity) * ((1 - (u_solution ** 2)) / u_solution) * (1 - (r_values / R) ** 2)
  • ナビエ・ストークス方程式の解から、円管内の各位置での速度分布を計算します。

結果をグラフ化

1
2
3
4
5
6
7
plt.figure(figsize=(8, 6))
plt.plot(r_values, u_values)
plt.xlabel('Radius')
plt.ylabel('Velocity')
plt.title('Velocity Distribution in Pipe Flow')
plt.grid(True)
plt.show()
  • matplotlibを使用して、計算された速度分布を円管の半径に対する速度としてグラフ化します。
    plt.xlabel、plt.ylabel、plt.titleを使用して、軸のラベルとグラフのタイトルを設定し、plt.grid(True)でグリッドを表示します。
    plt.show()でグラフを表示します。

このコードは、ナビエ・ストークス方程式を使用して円管内の流れにおける速度分布を解析し、その結果を可視化するものです。

グラフ解説

このグラフは円管内の流れにおける速度分布を示しています。

[実行結果]

x軸は円管の半径を示し、y軸はその位置における流速を表しています。

解析した速度分布は、理想的な流れ条件を仮定しています。
円管内の中心$ （r=0）$では、流速は最大になります。
そして、円管の壁に近づくにつれて流速はゼロに近づきます。

この結果は、円管内の流れにおいて、中心部分の流れが最も速く、壁に近づくほど流速が低くなることを示しています。
このような速度分布は、レイノルズ数や流体の粘度などの条件によって変化する可能性がありますが、円管流れの一般的な傾向を示しています。

また、このグラフは円管内の速度分布が放射状に変化していることを示しています。
中心部から外側に向かって流速が減少していることが分かります。
このような速度プロファイルは、流体が壁面で摩擦を受けることによって生じる、粘性効果によるものです。