非線形の最適化問題 SciPy

非線形の最適化問題

非線形の最適化問題を解くためには、SciPyライブラリのminimize()関数を使用します。

ここでは、簡単な非線形の最適化問題を解いてみます。

例として、次の非線形関数を最小化する問題を考えます。

$$
f(x) = x^2 + 5 \sin(x)
$$

この関数を最小化する$ (x) $の値を見つけることを目指します。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
import numpy as np
from scipy.optimize import minimize
import matplotlib.pyplot as plt

# 最小化する非線形関数
def objective_function(x):
    return x**2 + 5 * np.sin(x)

# 初期値
x0 = 0

# 最適化の実行
result = minimize(objective_function, x0, method='BFGS')

# 結果の表示
print("Optimal solution:", result.x)

# グラフ化
x_vals = np.linspace(-10, 10, 100)
y_vals = objective_function(x_vals)

plt.plot(x_vals, y_vals, label='Objective Function')
plt.scatter(result.x, objective_function(result.x), color='red', label='Optimal Solution')
plt.xlabel('x')
plt.ylabel('f(x)')
plt.title('Nonlinear Optimization')
plt.legend()
plt.grid(True)
plt.show()

このコードは、minimize()関数を使用して非線形関数を最小化しています。

関数の最小値を求めるためにBFGS（Broyden-Fletcher-Goldfarb-Shanno）最適化手法を使用しています。

最適解は result.x に格納されます。

また、matplotlibライブラリを使用して、非線形関数をグラフ化しています。

最小値の位置を赤色の点で表示しています。

ソースコード解説

このコードは、PythonのSciPyライブラリを使用して非線形最適化問題を解くものです。

  1. numpyおよびscipy.optimizeから必要なライブラリをインポートしています。
    また、グラフを描画するためにmatplotlib.pyplotもインポートしています。

  2. objective_function(x)という関数を定義しています。
    これは最小化する非線形関数です。
    ここでは$ ( f(x) = x^2 + 5 \sin(x) ) $となっています。

  3. 初期値 x0 を 0 としています。
    最適化アルゴリズムはこの初期値から始まり、関数の最小値を見つけようとします。

  4. minimize()関数を使用して、objective_functionを最小化します。
    ここでは** BFGS（Broyden-Fletcher-Goldfarb-Shanno）法 **を使用しています。

  5. result.xには、最適化アルゴリズムによって見つけられた最適解が格納されます。

  6. グラフ化のために、np.linspace()を使用して$ ( x ) $の値を範囲$ [-10, 10] $で生成し、それに対応する$ ( f(x) ) $の値を計算しています。

  7. plt.plot()を使って非線形関数を青色の折れ線グラフでプロットし、plt.scatter()を使って最適解の位置を赤い点で表示しています。

  8. 最後に、グラフの軸ラベル、タイトル、凡例、グリッドを設定し、plt.show()でグラフを表示しています。

このコードは、非線形最適化問題を解く手法とその結果を可視化する方法を示しています。

関数の最小値を見つけ、最適解の位置を視覚的に示すためにグラフを使用しています。

結果解説

この非線形関数$ ( f(x) = x^2 + 5 \sin(x) ) $を最小化するために、Scipyのminimize()関数を使用しました。

最適化手法としてはBFGS法を選択しました。

結果として得られた最適解は$ ( x \approx -1.11051052 ) $です。

この$ ( x ) $の値が関数$ ( f(x) ) $を最小化する点です。

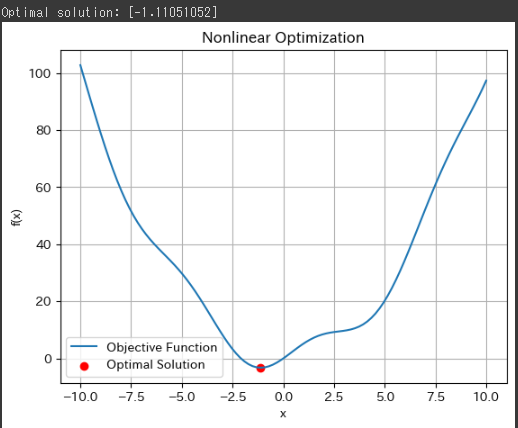
グラフでは、横軸が$ ( x )$、縦軸が$ ( f(x) ) $となっており、非線形関数が青線で表示されています。

赤い点が求められた最適解の位置を示しています。

この点は、関数が最小値を取る位置を表しています。

関数$ ( f(x) ) は ( x \approx -1.11051052 ) $の位置で最小値を持ちます。

この値は、関数が最小となる$ ( x ) $の位置を示しており、BFGS最適化アルゴリズムがこの値を見つけることができたことを示しています。