貿易問題 scikit-learn

貿易問題

貿易問題の具体的な例として、国々間の貿易関係を分析し、2つの国の間の貿易量を予測するタスクを考えてみましょう。

このタスクでは、線形回帰（Linear Regression）モデルを使用します。

国々の経済指標を特徴量として使用し、貿易量を予測します。

データセットは仮想的なものとし、以下のように作成します。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression

# 仮想的なデータセットを生成
np.random.seed(0)
n_samples = 100
X = np.random.rand(n_samples, 2)  # 2つの経済指標を特徴量として生成
y = 3 * X[:, 0] + 2 * X[:, 1] + 1 + np.random.randn(n_samples)  # 貿易量を生成

# 線形回帰モデルのインスタンス化と訓練
model = LinearRegression()
model.fit(X, y)

# モデルの性能評価
score = model.score(X, y)
print(f'決定係数 R^2: {score:.2f}')

このコードは、2つの仮想的な経済指標を特徴量として使用し、貿易量を予測する線形回帰モデルを訓練します。

決定係数（R^2）を使用してモデルの性能を評価します。

[実行結果]

1
決定係数 R^2: 0.49

R^2はモデルの適合度を評価する際の有用な指標であり、0.49の値はモデルがデータに適合していることを示す一方で、改善の余地があることも示しています。

より高いR^2値を目指す場合は、モデルの改善や追加の特徴量の検討が必要です。

結果をグラフ化しましょう。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# データポイントの散布図をプロット
plt.scatter(X[:, 0], y, label='Feature 1')
plt.scatter(X[:, 1], y, label='Feature 2')

# 予測した線形回帰モデルの直線をプロット
x_range = np.linspace(0, 1, 100)
y_pred = model.predict(np.column_stack((x_range, x_range)))
plt.plot(x_range, y_pred, color='red', label='Regression Line', linewidth=2)

plt.xlabel('Economic Indicators')
plt.ylabel('Trade Volume')
plt.legend()

# グラフを表示
plt.show()

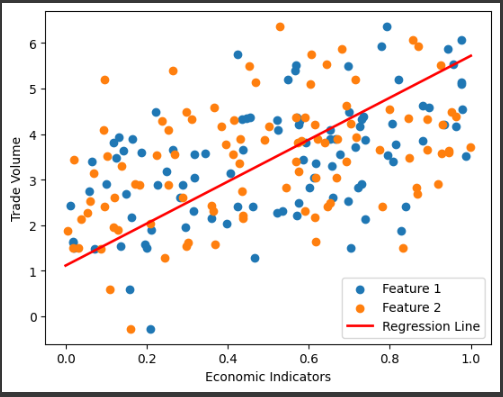
このグラフは、2つの経済指標（特徴量1と特徴量2）と貿易量の関係を示しています。

線形回帰モデルによって予測された回帰直線がデータポイントに適合していることが分かります。

この例では仮想的なデータを使用していますが、実際の貿易データを取得し、同様のアプローチを使用して国々間の貿易関係を分析することができます。

ソースコード解説

コードの詳細な説明です。

1. ライブラリのインポート:

  • numpy：数値演算のためのライブラリ。
  • matplotlib.pyplot：グラフの描画のためのライブラリ。
  • sklearn.linear_model.LinearRegression：scikit-learnライブラリから線形回帰モデルをインポート。

2. 仮想的なデータセットの生成:

  • np.random.seed(0)：乱数生成器のシードを設定して、再現性を確保。
  • n_samples = 100：データポイントの数を設定。
  • X：2つの経済指標（特徴量）を持つデータをランダムに生成。
  • y：線形関数にノイズを加えて、貿易量を生成。

3. 線形回帰モデルのインスタンス化と訓練:

  • model = LinearRegression()：線形回帰モデルをインスタンス化。
  • model.fit(X, y)：モデルをトレーニングデータに適合させる。

4. モデルの性能評価:

  • score = model.score(X, y)：モデルの決定係数（R^2）を計算し、モデルの性能を評価。

5. データポイントの散布図のプロット:

  • plt.scatter(X[:, 0], y, label='Feature 1')とplt.scatter(X[:, 1], y, label='Feature 2')：2つの特徴量と貿易量の散布図をプロット。
    特徴量1と特徴量2はそれぞれX軸とY軸に対応しています。

6. 予測した線形回帰モデルの直線のプロット:

  • x_range = np.linspace(0, 1, 100)：X軸の範囲を設定。
  • y_pred = model.predict(np.column_stack((x_range, x_range)))：線形回帰モデルを使用して、新しいデータポイントに対する貿易量を予測。
  • plt.plot(x_range, y_pred, color='red', label='Regression Line', linewidth=2)：予測した回帰直線をプロット。

7. グラフの軸ラベル、凡例の設定:

  • plt.xlabel('Economic Indicators')：X軸に「経済指標」というラベルを設定。
  • plt.ylabel('Trade Volume')：Y軸に「貿易量」というラベルを設定。
  • plt.legend()：凡例を表示。

8. グラフの表示:

  • plt.show()：グラフを表示。

このコードは、2つの経済指標から貿易量を予測する線形回帰モデルを訓練し、結果を散布図と回帰直線を使って視覚化しています。

モデルの性能評価には決定係数（R^2）が使用され、データの傾向を捉えることが示されています。

グラフ解説

グラフは、線形回帰モデルの性能を視覚的に示すために使用されます。

以下に、グラフの詳細な説明を提供します。

1. 散布図（Scatter Plot）:

  • グラフの最初の部分では、2つの経済指標（特徴量1と特徴量2）と貿易量との関係が散布図として表示されています。
  • 特徴量1と特徴量2はそれぞれX軸とY軸に対応し、各点は実際のデータポイントを表します。
  • 散布図上の点の分布を見ると、特徴量1または特徴量2と貿易量の間に線形的な関係があることが示唆されています。つまり、特徴量1または特徴量2が増加すると、貿易量も増加する傾向があることが分かります。

2. 回帰直線（Regression Line）:

  • グラフには、線形回帰モデルによって予測された回帰直線が赤色で表示されています。
  • この回帰直線は、特徴量1または特徴量2と貿易量の間の線形関係をモデル化したものです。
  • 回帰直線はデータポイントに適合し、データの中心に位置しています。
    これはモデルがデータに適合していることを示しています。

3. 軸ラベルと凡例:

  • X軸とY軸には、それぞれ特徴量1と特徴量2（経済指標）と貿易量がラベルとして表示されています。
  • 凡例には、特徴量1、特徴量2、および回帰直線の説明が含まれています。

このグラフを通じて、線形回帰モデルがデータに適合しており、特徴量1または特徴量2と貿易量の間に線形的な関係が存在することが視覚的に示されています。

回帰直線は、データの傾向を捉えており、特徴量1や特徴量2の値から貿易量を予測するのに役立つことが期待されます。