線形回帰② (データ準備)

重回帰問題を解くのに適したボストンの住宅価格データを準備します。

データの読み込み

まずはデータを読み込みます。(2行目)

読み込んだデータをデータフレームに格納し(5行目)、目的変数の項目名は“MEDV”とします。(6行目)

[Google Colaboratory]

1
2
3
4
5
6
7
8
from sklearn.datasets import load_boston
boston = load_boston()

import pandas as pd
df = pd.DataFrame(boston.data,columns=boston.feature_names)
df["MEDV"] = boston.target

display(df.head())

[実行結果]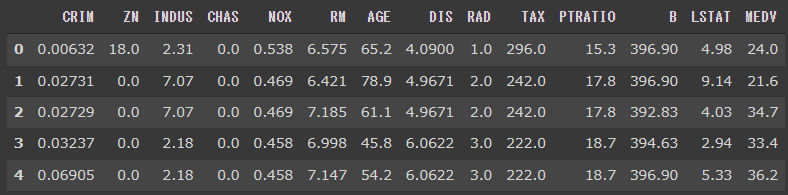

ホールドアウト法

説明変数を変数 Xに代入し、目的変数を変数 yに代入します。

今回は、説明変数に13種類全ての変数を使用することにします。

[Google Colaboratory]

1
2
3
4
5
X = df[boston.feature_names]
y = df[["MEDV"]]

display(X.head())
display(y.head())

[実行結果]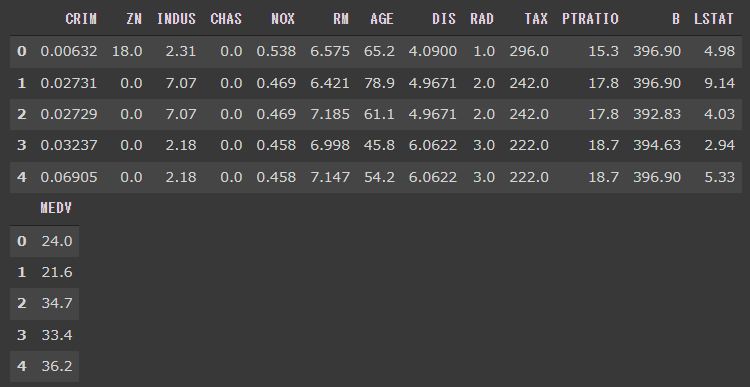

ホールドアウト法で、訓練データとテストデータに分割します。(2行目)

test_size=0.3と指定しているので、訓練データが70%、テストデータが30%の割合に分割されます。

[Google Colaboratory]

1
2
3
4
5
6
7
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y,test_size=0.3,random_state=0)

print(len(X_train))
display(X_train.head())
print(len(X_test))
display(X_test.head())

[実行結果]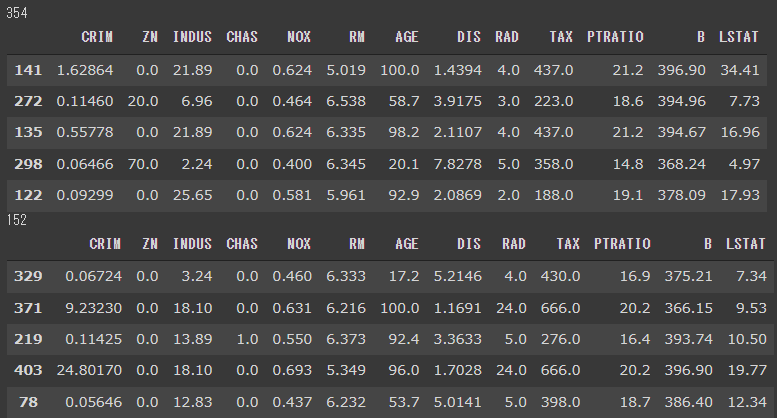

スケーリング

データのスケーリングを行います。

スケーリングとは、複数の説明変数間でのデータの尺度をそろえることを意味します。

重回帰のような複数の説明変数を扱う線形系のアルゴリズムは、データの尺度による影響を特に受けやすいため、正しく学習させるためにはデータのスケーリングが必要になります。

スケーリングには、主に次のような手法があります。

  • 標準化
    説明変数の平均が0、標準偏差が1になるようにスケーリングを行います。
    正規分布に従うデータに有効です。
  • 正規化
    説明変数の値が0～1の範囲に収まるようにスケーリングを行います。
    一様分布のようなデータに有効です。

正規分布でも一様分布でもない場合は、ロバストZスコアという手法が用いられることがあります。

スケーリングには明確な正解はなく、モデル精度と合わせて検討していくことが多くなります。


sklearnには、スケーリングをするためのクラスがありますのでこれを利用します。

[Google Colaboratory]

1
2
3
4
5
6
7
8
from sklearn.preprocessing import StandardScaler

scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)

print(X_train_scaled[:3])
print(X_test_scaled[:3])

fit_transform関数ではfit関数とtransform関数をまとめて実行します。(4行目)

transform関数では、fit関数の実行した結果を用いて、実際に正規化を 実行します 。(5行目)

訓練データにはfit_transform関数を使い、テストデータにはtransform関数を使うと覚えておくとよいでしょう。

[実行結果]

以上で、モデル構築の準備ができました。

次回は、今回準備したデータを使って重回帰モデルの構築を行います。