多変数・連続値で示される情報の表形式表現「CartPole」

CartPoleの状態を1つの変数に落とし込みます。

まずCartPoleの状態は次の４つの情報で表現されます。

変数 説明
カート位置 -2.4～2.4
カート速度 -Inf～Inf
棒の角度 -41.8°～41.8°
棒の角速度 -Inf～Inf

これら４つの情報は連続値となります。
連続値のままですとQ関数を用いて表形式で表現できません。

表形式で表現するために、連続値を離散化してデジタル化します。

離散化とは、連続した値を不連続な値に分割することです
例えばカート位置を6つの値(0～5)で離散化する場合には、-2.4～-1.6の場合は0、-1.6～-0.8の場合は1・・・というように変換します。
また-2.4を超えてマイナスになる可能性もあるので-Inf～-1.6を0とし、1.6～-Infを5とします。
変換後の0～5の値は離散変数と呼ばれます。

ほかの３つの情報も6つの値で離散化しますと変数が4種類ありますので6の4乗、つまり1296種類のデジタル値で表現できることになります。

CartPoleでとれる行動はカートを右に押すか、カートを左に押すの2通りですのでCartPoleのQ関数は1296行×2列の表形式で表現できます。
Q関数は各状態で各行動をとったときにその後得られる予定の割引報酬和を表します。

では状態の離散化を実装していきます。
ますは使用するパッケージをインポートします。

1
2
3
4
5
# 使用するパッケージの宣言
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
import gym

定数を定義します。

1
2
3
# 定数の設定
ENV = 'CartPole-v0'  # 使用する課題名
NUM_DIZITIZED = 6  # 各状態の離散値への分割数

CartPoleを実行し、環境の初期状態を取得します。

1
2
3
# CartPoleを実行してみる
env = gym.make(ENV)  # 実行する課題を設定
observation = env.reset()  # 環境の初期化

離散化の閾値を計算する関数を定義します。

1
2
3
4
# 離散化の閾値を求める
def bins(clip_min, clip_max, num):
    '''観測した状態（連続値）を離散値にデジタル変換する閾値を求める'''
    return np.linspace(clip_min, clip_max, num + 1)[1:-1]

np.linspace()関数は等間隔の数列を生成する命令です。
動作確認のための下記のコードを実行します。

1
np.linspace(-2.4, 2.4, 6 + 1)

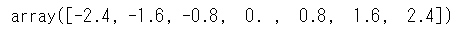
実行結果1

閾値としましては上記で得られる配列の最初と最後の要素は不要なのでスライスします。

1
np.linspace(-2.4, 2.4, 6 + 1)[1:-1]

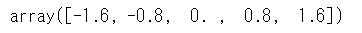
実行結果2

bins()関数で求めた閾値に応じて、連続変数を離散化する関数を作成します。4変数を一度に変換します。
np.digitizeは状態変数のリストをbinsに応じてデジタル値に変換します。

最後に4つの離散変数を6進数で計算しreturnしています。

1
2
3
4
5
6
7
8
9
10
def digitize_state(observation):
    '''観測したobservation状態を、離散値に変換する'''
    cart_pos, cart_v, pole_angle, pole_v = observation
    digitized = [
        np.digitize(cart_pos, bins=bins(-2.4, 2.4, NUM_DIZITIZED)),
        np.digitize(cart_v, bins=bins(-3.0, 3.0, NUM_DIZITIZED)),
        np.digitize(pole_angle, bins=bins(-0.5, 0.5, NUM_DIZITIZED)),
        np.digitize(pole_v, bins=bins(-2.0, 2.0, NUM_DIZITIZED))]
    print('digitized', digitized)
    return sum([x * (NUM_DIZITIZED**i) for i, x in enumerate(digitized)])

動作確認のためdigitize_state()関数をコールして結果を確認します。

1
print('digitize_state', digitize_state(observation))

実行結果3

CartPoleの状態を離散化し表形式表現できましたので、次回はQ学習を実装しCartPoleを制御していきます。


参考 > つくりながら学ぶ！深層強化学習 サポートページ