強化学習 AlphaZero 19 (リバーシ)

AlphaZeroのアルゴリズムを使ってリバーシの対戦ゲームを作ります。

リバーシは相手の石をはさむと自分の石の色に変わり、最終的に石の多い方が勝ちとなります。

ソースコード一覧は下記のようになります。

ソースコード 説明 ３目並べとの相違
game.py ゲーム状態 全て
dual_network.py デュアルネットワーク パラメータのみ
pv_mcts.py モンテカルロ木探索 なし
self_play.py セルフプレイ部 なし
train_network.py パラメータ更新部 なし
evaluate_network.py 新パラメータ評価部 なし
train_cycle.py 学習サイクルの実行 ベストプレイヤーの評価を削除
human_play.py ゲームUI 全て

まずリバーシのゲーム状態を作成します。

game.py
1
2
3
4
5
6
7
8
9
10
# ====================
# リバーシ
# ====================

# パッケージのインポート
import random
import math

# ゲーム状態
class State:

ゲーム状態の初期化を行います。
「自分の石の配置」「相手の石の配置」を長さ３６（６列×６行）の１次元配列で保持します。
石の初期配置は中央に交差するように２枚ずつ石を置きます。

各変数の意味は下記の通りです。

  • depthは何ターン目かを表します。
  • pass_endは連続パスによる終了を示すフラグです。
  • dxyは８方向を示す方向定数です。
game.py
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
# 初期化
def __init__(self, pieces=None, enemy_pieces=None, depth=0):
    # 方向定数
    self.dxy = ((1, 0), (1, 1), (0, 1), (-1, 1), (-1, 0), (-1, -1), (0, -1), (1, -1))

    # 連続パスによる終了
    self.pass_end = False

    # 石の配置
    self.pieces = pieces
    self.enemy_pieces = enemy_pieces
    self.depth = depth

    # 石の初期配置
    if pieces == None or enemy_pieces == None:
        self.pieces = [0] * 36
        self.pieces[14] = self.pieces[21] = 1
        self.enemy_pieces = [0] * 36
        self.enemy_pieces[15] = self.enemy_pieces[20] = 1

石の数を取得する関数です。

game.py
1
2
3
4
5
6
7
# 石の数の取得
def piece_count(self, pieces):
    count = 0
    for i in pieces:
        if i == 1:
            count +=  1
    return count

負けかどうかを判定します。

game.py
1
2
3
# 負けかどうか
def is_lose(self):
    return self.is_done() and self.piece_count(self.pieces) < self.piece_count(self.enemy_pieces)

引き分けかどうかを判定します。

game.py
1
2
3
# 引き分けかどうか
def is_draw(self):
    return self.is_done() and self.piece_count(self.pieces) == self.piece_count(self.enemy_pieces)

ゲーム終了かどうかを判定します。

game.py
1
2
3
# ゲーム終了かどうか
def is_done(self):
    return self.piece_count(self.pieces) + self.piece_count(self.enemy_pieces) == 36 or self.pass_end

行動に応じた次の状態を取得します。

game.py
1
2
3
4
5
6
7
8
9
10
11
12
13
# 次の状態の取得
def next(self, action):
    state = State(self.pieces.copy(), self.enemy_pieces.copy(), self.depth+1)
    if action != 36:
        state.is_legal_action_xy(action%6, int(action/6), True)
    w = state.pieces
    state.pieces = state.enemy_pieces
    state.enemy_pieces = w

    # 2回連続パス判定
    if action == 36 and state.legal_actions() == [36]:
        state.pass_end = True
    return state

合法手のリストを取得します。

game.py
1
2
3
4
5
6
7
8
9
10
# 合法手のリストの取得
def legal_actions(self):
    actions = []
    for j in range(0,6):
        for i in range(0,6):
            if self.is_legal_action_xy(i, j):
                actions.append(i+j*6)
    if len(actions) == 0:
        actions.append(36) # パス
    return actions

任意のマスが合法手かどうかを取得します。
引数のx,yはマスのXY座標、flipは挟んだ石を裏がえすかどうかということになります。

game.py
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
# 任意のマスが合法手かどうか
def is_legal_action_xy(self, x, y, flip=False):
    # 任意のマスの任意の方向が合法手かどうか
    def is_legal_action_xy_dxy(x, y, dx, dy):
        # １つ目 相手の石
        x, y = x+dx, y+dy
        if y < 0 or 5 < y or x < 0 or 5 < x or \
            self.enemy_pieces[x+y*6] != 1:
            return False

        # 2つ目以降
        for j in range(6):
            # 空
            if y < 0 or 5 < y or x < 0 or 5 < x or \
                (self.enemy_pieces[x+y*6] == 0 and self.pieces[x+y*6] == 0):
                return False

            # 自分の石
            if self.pieces[x+y*6] == 1:
                # 反転
                if flip:
                    for i in range(6):
                        x, y = x-dx, y-dy
                        if self.pieces[x+y*6] == 1:
                            return True
                        self.pieces[x+y*6] = 1
                        self.enemy_pieces[x+y*6] = 0
                return True
            # 相手の石
            x, y = x+dx, y+dy
        return False

    # 空きなし
    if self.enemy_pieces[x+y*6] == 1 or self.pieces[x+y*6] == 1:
        return False

    # 石を置く
    if flip:
        self.pieces[x+y*6] = 1

    # 任意の位置が合法手かどうか
    flag = False
    for dx, dy in self.dxy:
        if is_legal_action_xy_dxy(x, y, dx, dy):
            flag = True
    return flag

先手かどうかを取得します。

game.py
1
2
3
# 先手かどうか
def is_first_player(self):
    return self.depth%2 == 0

ゲーム状態の文字表示を行います。

game.py
1
2
3
4
5
6
7
8
9
10
11
12
13
14
# 文字列表示
def __str__(self):
    ox = ('o', 'x') if self.is_first_player() else ('x', 'o')
    str = ''
    for i in range(36):
        if self.pieces[i] == 1:
            str += ox[0]
        elif self.enemy_pieces[i] == 1:
            str += ox[1]
        else:
            str += '-'
        if i % 6 == 5:
            str += '\n'
    return str

ランダム対ランダムで対戦するコードを実装します。

game.py
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
# ランダムで行動選択
def random_action(state):
    legal_actions = state.legal_actions()
    return legal_actions[random.randint(0, len(legal_actions)-1)]

# 動作確認
if __name__ == '__main__':
    # 状態の生成
    state = State()

    # ゲーム終了までのループ
    while True:
        # ゲーム終了時
        if state.is_done():
            break

        # 次の状態の取得
        state = state.next(random_action(state))

        # 文字列表示
        print(state)
        print()

試しに実行したところ下記のような結果となりました。

最終結果（途中略）

次にデュアルネットワークを実装します。
入力シェイプと行動数のパラメータのみ変更しています。
入力シェイプは、自分の石の配置(6x6)と相手の石の配置(6x6)となります。
行動数は３７（配置先6x6 + 合法手がないためのパス）となります。

dual_network.py
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
# ====================
# デュアルネットワークの作成
# ====================

# パッケージのインポート
from tensorflow.keras.layers import Activation, Add, BatchNormalization, Conv2D, Dense, GlobalAveragePooling2D, Input
from tensorflow.keras.models import Model
from tensorflow.keras.regularizers import l2
from tensorflow.keras import backend as K
import os

# パラメータの準備
DN_FILTERS  = 128 # 畳み込み層のカーネル数（本家は256）
DN_RESIDUAL_NUM =  16 # 残差ブロックの数（本家は19）
DN_INPUT_SHAPE = (6, 6, 2) # 入力シェイプ
DN_OUTPUT_SIZE = 37 # 行動数(配置先(6*6)+パス(1))

# 畳み込み層の作成
def conv(filters):
    return Conv2D(filters, 3, padding='same', use_bias=False,
        kernel_initializer='he_normal', kernel_regularizer=l2(0.0005))

# 残差ブロックの作成
def residual_block():
    def f(x):
        sc = x
        x = conv(DN_FILTERS)(x)
        x = BatchNormalization()(x)
        x = Activation('relu')(x)
        x = conv(DN_FILTERS)(x)
        x = BatchNormalization()(x)
        x = Add()([x, sc])
        x = Activation('relu')(x)
        return x
    return f

# デュアルネットワークの作成
def dual_network():
    # モデル作成済みの場合は無処理
    if os.path.exists('./model/best.h5'):
        return

    # 入力層
    input = Input(shape=DN_INPUT_SHAPE)

    # 畳み込み層
    x = conv(DN_FILTERS)(input)
    x = BatchNormalization()(x)
    x = Activation('relu')(x)

    # 残差ブロック x 16
    for i in range(DN_RESIDUAL_NUM):
        x = residual_block()(x)

    # プーリング層
    x = GlobalAveragePooling2D()(x)

    # ポリシー出力
    p = Dense(DN_OUTPUT_SIZE, kernel_regularizer=l2(0.0005),
                activation='softmax', name='pi')(x)

    # バリュー出力
    v = Dense(1, kernel_regularizer=l2(0.0005))(x)
    v = Activation('tanh', name='v')(v)

    # モデルの作成
    model = Model(inputs=input, outputs=[p,v])

    # モデルの保存
    os.makedirs('./model/', exist_ok=True) # フォルダがない時は生成
    model.save('./model/best.h5') # ベストプレイヤーのモデル

    # モデルの破棄
    K.clear_session()
    del model

モンテカルロ木探索を実装します。変更はありません。

pv_mcts.py
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
# ====================
# モンテカルロ木探索の作成
# ====================

# パッケージのインポート
from game import State
from dual_network import DN_INPUT_SHAPE
from math import sqrt
from tensorflow.keras.models import load_model
from pathlib import Path
import numpy as np

# パラメータの準備
PV_EVALUATE_COUNT = 50 # 1推論あたりのシミュレーション回数（本家は1600）

# 推論
def predict(model, state):
    # 推論のための入力テ゛ータのシェイフ゜の変換
    a, b, c = DN_INPUT_SHAPE
    x = np.array([state.pieces, state.enemy_pieces])
    x = x.reshape(c, a, b).transpose(1, 2, 0).reshape(1, a, b, c)

    # 推論
    y = model.predict(x, batch_size=1)

    # 方策の取得
    policies = y[0][0][list(state.legal_actions())] # 合法手のみ
    policies /= sum(policies) if sum(policies) else 1 # 合計1の確率分布に変換

    # 価値の取得
    value = y[1][0][0]
    return policies, value

# ノードのリストを試行回数のリストに変換
def nodes_to_scores(nodes):
    scores = []
    for c in nodes:
        scores.append(c.n)
    return scores

# モンテカルロ木探索のスコアの取得
def pv_mcts_scores(model, state, temperature):
    # モンテカルロ木探索のノードの定義
    class Node:
        # ノードの初期化
        def __init__(self, state, p):
            self.state = state # 状態
            self.p = p # 方策
            self.w = 0 # 累計価値
            self.n = 0 # 試行回数
            self.child_nodes = None  # 子ノード群

        # 局面の価値の計算
        def evaluate(self):
            # ゲーム終了時
            if self.state.is_done():
                # 勝敗結果で価値を取得
                value = -1 if self.state.is_lose() else 0

                # 累計価値と試行回数の更新
                self.w += value
                self.n += 1
                return value

            # 子ノードが存在しない時
            if not self.child_nodes:
                # ニューラルネットワークの推論で方策と価値を取得
                policies, value = predict(model, self.state)

                # 累計価値と試行回数の更新
                self.w += value
                self.n += 1

                # 子ノードの展開
                self.child_nodes = []
                for action, policy in zip(self.state.legal_actions(), policies):
                    self.child_nodes.append(Node(self.state.next(action), policy))
                return value

            # 子ノードが存在する時
            else:
                # アーク評価値が最大の子ノードの評価で価値を取得
                value = -self.next_child_node().evaluate()

                # 累計価値と試行回数の更新
                self.w += value
                self.n += 1
                return value

        # アーク評価値が最大の子ノードを取得
        def next_child_node(self):
            # アーク評価値の計算
            C_PUCT = 1.0
            t = sum(nodes_to_scores(self.child_nodes))
            pucb_values = []
            for child_node in self.child_nodes:
                pucb_values.append((-child_node.w / child_node.n if child_node.n else 0.0) +
                    C_PUCT * child_node.p * sqrt(t) / (1 + child_node.n))

            # アーク評価値が最大の子ノードを返す
            return self.child_nodes[np.argmax(pucb_values)]

    # 現在の局面のノードの作成
    root_node = Node(state, 0)

    # 複数回の評価の実行
    for _ in range(PV_EVALUATE_COUNT):
        root_node.evaluate()

    # 合法手の確率分布
    scores = nodes_to_scores(root_node.child_nodes)
    if temperature == 0: # 最大値のみ1
        action = np.argmax(scores)
        scores = np.zeros(len(scores))
        scores[action] = 1
    else: # ボルツマン分布でバラつき付加
        scores = boltzman(scores, temperature)
    return scores

# モンテカルロ木探索で行動選択
def pv_mcts_action(model, temperature=0):
    def pv_mcts_action(state):
        scores = pv_mcts_scores(model, state, temperature)
        return np.random.choice(state.legal_actions(), p=scores)
    return pv_mcts_action

# ボルツマン分布
def boltzman(xs, temperature):
    xs = [x ** (1 / temperature) for x in xs]
    return [x / sum(xs) for x in xs]

セルフプレイを実装します。変更はありません。

self_play.py
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
# ====================
# セルフプレイ部
# ====================

# パッケージのインポート
from game import State
from pv_mcts import pv_mcts_scores
from dual_network import DN_OUTPUT_SIZE
from datetime import datetime
from tensorflow.keras.models import load_model
from tensorflow.keras import backend as K
from pathlib import Path
import numpy as np
import pickle
import os

# パラメータの準備
SP_GAME_COUNT = 500 # セルフプレイを行うゲーム数（本家は25000）
SP_TEMPERATURE = 1.0 # ボルツマン分布の温度パラメータ

# 先手プレイヤーの価値
def first_player_value(ended_state):
    # 1:先手勝利, -1:先手敗北, 0:引き分け
    if ended_state.is_lose():
        return -1 if ended_state.is_first_player() else 1
    return 0

# 学習データの保存
def write_data(history):
    now = datetime.now()
    os.makedirs('./data/', exist_ok=True) # フォルダがない時は生成
    path = './data/{:04}{:02}{:02}{:02}{:02}{:02}.history'.format(
        now.year, now.month, now.day, now.hour, now.minute, now.second)
    with open(path, mode='wb') as f:
        pickle.dump(history, f)

# 1ゲームの実行
def play(model):
    # 学習データ
    history = []

    # 状態の生成
    state = State()

    while True:
        # ゲーム終了時
        if state.is_done():
            break

        # 合法手の確率分布の取得
        scores = pv_mcts_scores(model, state, SP_TEMPERATURE)

        # 学習データに状態と方策を追加
        policies = [0] * DN_OUTPUT_SIZE
        for action, policy in zip(state.legal_actions(), scores):
            policies[action] = policy
        history.append([[state.pieces, state.enemy_pieces], policies, None])

        # 行動の取得
        action = np.random.choice(state.legal_actions(), p=scores)

        # 次の状態の取得
        state = state.next(action)

    # 学習データに価値を追加
    value = first_player_value(state)
    for i in range(len(history)):
        history[i][2] = value
        value = -value
    return history

# セルフプレイ
def self_play():
    # 学習データ
    history = []

    # ベストプレイヤーのモデルの読み込み
    model = load_model('./model/best.h5')

    # 複数回のゲームの実行
    for i in range(SP_GAME_COUNT):
        # 1ゲームの実行
        h = play(model)
        history.extend(h)

        # 出力
        print('\rSelfPlay {}/{}'.format(i+1, SP_GAME_COUNT), end='')
    print('')

    # 学習データの保存
    write_data(history)

    # モデルの破棄
    K.clear_session()
    del model

パラメータ更新部を実装します。変更はありません。

train_network.py
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
# ====================
# パラメータ更新部
# ====================

# パッケージのインポート
from dual_network import DN_INPUT_SHAPE
from tensorflow.keras.callbacks import LearningRateScheduler, LambdaCallback
from tensorflow.keras.models import load_model
from tensorflow.keras import backend as K
from pathlib import Path
import numpy as np
import pickle

# パラメータの準備
RN_EPOCHS = 100 # 学習回数

# 学習データの読み込み
def load_data():
    history_path = sorted(Path('./data').glob('*.history'))[-1]
    with history_path.open(mode='rb') as f:
        return pickle.load(f)

# デュアルネットワークの学習
def train_network():
    # 学習データの読み込み
    history = load_data()
    xs, y_policies, y_values = zip(*history)

    # 学習のための入力テ゛ータのシェイフ゜の変換
    a, b, c = DN_INPUT_SHAPE
    xs = np.array(xs)
    xs = xs.reshape(len(xs), c, a, b).transpose(0, 2, 3, 1)
    y_policies = np.array(y_policies)
    y_values = np.array(y_values)

    # ベストプレイヤーのモデルの読み込み
    model = load_model('./model/best.h5')

    # モデルのコンパイル
    model.compile(loss=['categorical_crossentropy', 'mse'], optimizer='adam')

    # 学習率
    def step_decay(epoch):
        x = 0.001
        if epoch >= 50: x = 0.0005
        if epoch >= 80: x = 0.00025
        return x
    lr_decay = LearningRateScheduler(step_decay)

    # 出力
    print_callback = LambdaCallback(
        on_epoch_begin=lambda epoch,logs:
                print('\rTrain {}/{}'.format(epoch + 1,RN_EPOCHS), end=''))

    # 学習の実行
    model.fit(xs, [y_policies, y_values], batch_size=128, epochs=RN_EPOCHS,
            verbose=0, callbacks=[lr_decay, print_callback])
    print('')

    # 最新プレイヤーのモデルの保存
    model.save('./model/latest.h5')

    # モデルの破棄
    K.clear_session()
    del model

新パラメータ評価部を実装します。変更はありません。

evaluate_network.py
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
# ====================
# 新パラメータ評価部
# ====================

# パッケージのインポート
from game import State
from pv_mcts import pv_mcts_action
from tensorflow.keras.models import load_model
from tensorflow.keras import backend as K
from pathlib import Path
from shutil import copy
import numpy as np

# パラメータの準備
EN_GAME_COUNT = 10 # 1評価あたりのゲーム数（本家は400）
EN_TEMPERATURE = 1.0 # ボルツマン分布の温度

# 先手プレイヤーのポイント
def first_player_point(ended_state):
    # 1:先手勝利, 0:先手敗北, 0.5:引き分け
    if ended_state.is_lose():
        return 0 if ended_state.is_first_player() else 1
    return 0.5

# 1ゲームの実行
def play(next_actions):
    # 状態の生成
    state = State()

    # ゲーム終了までループ
    while True:
        # ゲーム終了時
        if state.is_done():
            break;

        # 行動の取得
        next_action = next_actions[0] if state.is_first_player() else next_actions[1]
        action = next_action(state)

        # 次の状態の取得
        state = state.next(action)

    # 先手プレイヤーのポイントを返す
    return first_player_point(state)

# ベストプレイヤーの交代
def update_best_player():
    copy('./model/latest.h5', './model/best.h5')
    print('Change BestPlayer')

# ネットワークの評価
def evaluate_network():
    # 最新プレイヤーのモデルの読み込み
    model0 = load_model('./model/latest.h5')

    # ベストプレイヤーのモデルの読み込み
    model1 = load_model('./model/best.h5')

    # PV MCTSで行動選択を行う関数の生成
    next_action0 = pv_mcts_action(model0, EN_TEMPERATURE)
    next_action1 = pv_mcts_action(model1, EN_TEMPERATURE)
    next_actions = (next_action0, next_action1)

    # 複数回の対戦を繰り返す
    total_point = 0
    for i in range(EN_GAME_COUNT):
        # 1ゲームの実行
        if i % 2 == 0:
            total_point += play(next_actions)
        else:
            total_point += 1 - play(list(reversed(next_actions)))

        # 出力
        print('\rEvaluate {}/{}'.format(i + 1, EN_GAME_COUNT), end='')
    print('')

    # 平均ポイントの計算
    average_point = total_point / EN_GAME_COUNT
    print('AveragePoint', average_point)

    # モデルの破棄
    K.clear_session()
    del model0
    del model1

    # ベストプレイヤーの交代
    if average_point > 0.5:
        update_best_player()
        return True
    else:
        return False

学習サイクルを実行します。ベストプレイヤーの評価は削除しています。
この処理を実行するとベストプレイヤーのモデルが作成されます。(model/best.h5)

学習完了までにCorei5、メモリ4G、GPUなしのPCでまる２日ほどかかりました。

train_cycle.py
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
# ====================
# 学習サイクルの実行
# ====================

# パッケージのインポート
from dual_network import dual_network
from self_play import self_play
from train_network import train_network
from evaluate_network import evaluate_network

# デュアルネットワークの作成
dual_network()

for i in range(10):
    print('Train',i,'====================')
    # セルフプレイ部
    self_play()

    # パラメータ更新部
    train_network()

    # 新ハ゜ラメータ評価部
    evaluate_network()

ゲームUIを実装します。

human_play.py
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
# ====================
# 人とAIの対戦
# ====================

# パッケージのインポート
from game import State
from pv_mcts import pv_mcts_action
from tensorflow.keras.models import load_model
from pathlib import Path
from threading import Thread
import tkinter as tk

# ベストプレイヤーのモデルの読み込み
model = load_model('./model/best.h5')

# ゲームUIの定義
class GameUI(tk.Frame):

ゲームUIの初期化を行います。
下記の３つを用意します。

  • ゲームの状態
  • モンテカルロ木探索で行動選択を行う関数
  • キャンバス
human_play.py
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
# 初期化
def __init__(self, master=None, model=None):
    tk.Frame.__init__(self, master)
    self.master.title('リバーシ')

    # ゲーム状態の生成
    self.state = State()

    # PV MCTSで行動選択を行う関数の生成
    self.next_action = pv_mcts_action(model, 0.0)

    # キャンバスの生成
    self.c = tk.Canvas(self, width = 240, height = 240, highlightthickness = 0)
    self.c.bind('<Button-1>', self.turn_of_human)
    self.c.pack()

    # 描画の更新
    self.on_draw()

人間のターンの処理を行います。

  1. ゲーム終了時はゲーム状態を初期状態に戻します。
  2. 先手でない時、操作不可とします。
  3. クリック位置を行動に変換します。
  4. 合法手でない時、無処理とします。
  5. 合法手の場合、次の状態を取得して描画の更新を行います。
  6. AIのターンへの遷移を行います。
human_play.py
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
# 人間のターン
def turn_of_human(self, event):
    # ゲーム終了時
    if self.state.is_done():
        self.state = State()
        self.on_draw()
        return

    # 先手でない時
    if not self.state.is_first_player():
        return

    # クリック位置を行動に変換
    x = int(event.x/40)
    y = int(event.y/40)
    if x < 0 or 5 < x or y < 0 or 5 < y: # 範囲外
        return
    action = x + y * 6

    # 合法手でない時
    legal_actions = self.state.legal_actions()
    if legal_actions == [36]:
        action = 36 # パス
    if action != 36 and not (action in legal_actions):
        return

    # 次の状態の取得
    self.state = self.state.next(action)
    self.on_draw()

    # AIのターン
    self.master.after(1, self.turn_of_ai)

AIのターンの処理を行います。

  1. ゲーム終了時は無処理です。
  2. デュアルネットワークで行動を取得します。
  3. 取得した行動に応じて次の状態を取得し、描画の更新を行います。
human_play.py
1
2
3
4
5
6
7
8
9
10
11
12
# AIのターン
def turn_of_ai(self):
    # ゲーム終了時
    if self.state.is_done():
        return

    # 行動の取得
    action = self.next_action(self.state)

    # 次の状態の取得
    self.state = self.state.next(action)
    self.on_draw()

石の描画を行います。
引数のindexはマス番号、first_playerは先手かどうかを表します。
先手は赤色のマルで後手は白色のマルを表します。

human_play.py
1
2
3
4
5
6
7
8
# 石の描画
def draw_piece(self, index, first_player):
    x = (index%6)*40+5
    y = int(index/6)*40+5
    if first_player:
        self.c.create_oval(x, y, x+30, y+30, width = 1.0, outline = '#000000', fill = '#C2272D')
    else:
        self.c.create_oval(x, y, x+30, y+30, width = 1.0, outline = '#000000', fill = '#FFFFFF')

全てのマス目と石を描画します。

human_play.py
1
2
3
4
5
6
7
8
9
10
11
12
# 描画の更新
def on_draw(self):
    self.c.delete('all')
    self.c.create_rectangle(0, 0, 240, 240, width = 0.0, fill = '#C69C6C')
    for i in range(1, 8):
        self.c.create_line(0, i*40, 240, i*40, width = 1.0, fill = '#000000')
        self.c.create_line(i*40, 0, i*40, 240, width = 1.0, fill = '#000000')
    for i in range(36):
        if self.state.pieces[i] == 1:
            self.draw_piece(i, self.state.is_first_player())
        if self.state.enemy_pieces[i] == 1:
            self.draw_piece(i, not self.state.is_first_player())

ゲームUIを実行します。

human_play.py
1
2
3
4
# ゲームUIの実行
f = GameUI(model=model)
f.pack()
f.mainloop()

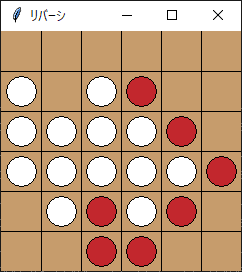
human_play.pyを実行するとリバーシが始まりAIと対戦することができます。

対戦中

なかなか強いAIとなっています。本気でやったのに負けました。

参考

AlphaZero 深層学習・強化学習・探索 人工知能プログラミング実践入門 サポートページ