強化学習 AlphaZero 5 (三目並べ ミニマックス法)

三目並べをミニマックス法で解いていきます。

ミニマックス法は、自分は自分にとって最善手を選び、相手は自分にとって最悪手を選ぶと仮定して最善手を探すアルゴリズムです。

ポイントは次の通りです。

  • next()は行動に応じて次の状態を取得する。
  • 行動は石を配置するマスの位置を０～８で指定する。
  • legal_actions()は選択可能な行動を取得します。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
# 三目並べの作成
import random

# ゲームの状態
class State:
    # 初期化
    def __init__(self, pieces=None, enemy_pieces=None):
        # 石の配置
        self.pieces = pieces if pieces != None else [0] * 9
        self.enemy_pieces = enemy_pieces if enemy_pieces != None else [0] * 9

    # 石の数の取得
    def piece_count(self, pieces):
        count = 0
        for i in pieces:
            if i == 1:
                count +=  1
        return count

    # 負けかどうか
    def is_lose(self):
        # 3並びかどうか
        def is_comp(x, y, dx, dy):
            for k in range(3):
                if y < 0 or 2 < y or x < 0 or 2 < x or \
                    self.enemy_pieces[x+y*3] == 0:
                    return False
                x, y = x+dx, y+dy
            return True

        # 負けかどうか
        if is_comp(0, 0, 1, 1) or is_comp(0, 2, 1, -1):
            return True
        for i in range(3):
            if is_comp(0, i, 1, 0) or is_comp(i, 0, 0, 1):
                return True
        return False

    # 引き分けかどうか
    def is_draw(self):
        return self.piece_count(self.pieces) + self.piece_count(self.enemy_pieces) == 9

    # ゲーム終了かどうか
    def is_done(self):
        return self.is_lose() or self.is_draw()

    # 次の状態の取得
    def next(self, action):
        pieces = self.pieces.copy()
        pieces[action] = 1
        return State(self.enemy_pieces, pieces)

    # 合法手のリストの取得
    def legal_actions(self):
        actions = []
        for i in range(9):
            if self.pieces[i] == 0 and self.enemy_pieces[i] == 0:
                actions.append(i)
        return actions

    # 先手かどうか
    def is_first_player(self):
        return self.piece_count(self.pieces) == self.piece_count(self.enemy_pieces)

    # 文字列表示
    def __str__(self):
        ox = ('o', 'x') if self.is_first_player() else ('x', 'o')
        str = ''
        for i in range(9):
            if self.pieces[i] == 1:
                str += ox[0]
            elif self.enemy_pieces[i] == 1:
                str += ox[1]
            else:
                str += '-'
            if i % 3 == 2:
                str += '\n'
        return str

ランダムで行動選択する関数を実装します。
leagl_actions()で合法手を取得し、その中からランダムに手を選びます。

1
2
3
4
# ランダムで行動選択
def random_action(state):
    legal_actions = state.legal_actions()
    return legal_actions[random.randint(0, len(legal_actions)-1)]

ランダムとランダムで三目並べを対戦させます。
ゲーム終了まで行動の取得と次の状態の取得を繰り返します。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
# ランダムとランダムで対戦

# 状態の生成
state = State()

# ゲーム終了までのループ
while True:
    # ゲーム終了時
    if state.is_done():
        break;

    # 行動の取得
    action = random_action(state)

    # 次の状態の取得
    state = state.next(action)

    # 文字列表示
    print(state)
    print()


結果

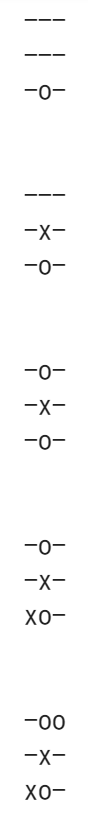
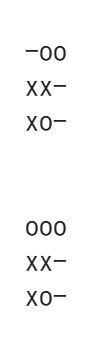
ミニマックス法で状態価値の計算を行います。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
# ミニマックス法で状態価値計算
def mini_max(state):
    # 負けは状態価値-1
    if state.is_lose():
        return -1
    
    # 引き分けは状態価値0
    if state.is_draw():
        return  0

    # 合法手の状態価値の計算
    best_score = -float('inf')
    for action in state.legal_actions():
        score = -mini_max(state.next(action))
        if score > best_score:
            best_score = score

    # 合法手の状態価値の最大値を返す
    return best_score

ミニマックス法で状態に応じて行動を返す関数を実装します。
Stateを渡すと行動（石を置くマス：０～８）を返します。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
# ミニマックス法で行動選択
def mini_max_action(state):
    # 合法手の状態価値の計算
    best_action = 0
    best_score = -float('inf')
    str = ['','']
    for action in state.legal_actions():
        score = -mini_max(state.next(action))
        if score > best_score:
            best_action = action
            best_score  = score
            
        str[0] = '{}{:2d},'.format(str[0], action)
        str[1] = '{}{:2d},'.format(str[1], score)
    print('action:', str[0], '\nscore: ', str[1], '\n')

    # 合法手の状態価値の最大値を持つ行動を返す
    return best_action

ミニマックス法とランダムで対戦します。
先手はmini_max_action()、後手はrandmo_action()を使います。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
# ミニマックス法とランダムで対戦

# 状態の生成
state = State()

# ゲーム終了までのループ
while True:
    # ゲーム終了時
    if state.is_done():
        break

    # 行動の取得
    if state.is_first_player():
        action = mini_max_action(state)
    else:
        action = random_action(state)
    
    # 次の状態の取得
    state = state.next(action)

    # 文字列表示
    print(state)
    print()

実行ごとに結果がかわるので複数回実行してみてください。
ただランダムが勝つことはありません。

結果

(Google Colaboratoryで動作確認しています。)

参考

AlphaZero 深層学習・強化学習・探索 人工知能プログラミング実践入門 サポートページ