強化学習 AlphaZero 3 (迷路ゲーム Sarsa/Q-learning)

迷路ゲームをSarsaとQ-learningで解いていきます。

SarsaとQ-learningは価値反復法と呼ばれ、ある行動をとるたびに状態価値を増やす手法です。
（Sarsaは収束が遅い一方局所解に陥りにくく、Q-learningは収束が早い一方で局所解に陥りやすいと言われています。）

今回の強化学習のポイントは下記です。

  • 目的はゴールすること。
  • 状態は位置。
  • 行動は上下左右の４種類。
  • 報酬はゴールしたら＋１。
  • パラメータl更新間隔は行動１回ごと。

価値反復法の学習手順は次の通りです。

  1. ランダム行動の準備する。
  2. 行動価値関数を準備する。
  3. 行動に従って、次の状態を取得する。
  4. ランダムまたは行動価値関数に従って、行動を取得する。
  5. 行動価値関数を更新する。
  6. ゴールするまで3～5を繰り返す。

まずは必要なパッケージをインポートします。

1
2
3
4
5
6
# パッケージのインポート
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
from matplotlib import animation
from IPython.display import HTML

迷路を作成します。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
# 迷路の作成
fig = plt.figure(figsize=(3, 3))

# 壁
plt.plot([0, 3], [3, 3], color='k')
plt.plot([0, 3], [0, 0], color='k')
plt.plot([0, 0], [0, 2], color='k')
plt.plot([3, 3], [1, 3], color='k')
plt.plot([1, 1], [1, 2], color='k')
plt.plot([2, 3], [2, 2], color='k')
plt.plot([2, 1], [1, 1], color='k')
plt.plot([2, 2], [0, 1], color='k')

# 数字
for i in range(3):
    for j in range(3):
        plt.text(0.5+i, 2.5-j, str(i+j*3), size=20, ha='center', va='center')

# 円
circle, = plt.plot([0.5], [2.5], marker='o', color='#d3d3d3', markersize=40)

# 目盛りと枠の非表示
plt.tick_params(axis='both', which='both', bottom='off', top= 'off',
        labelbottom='off', right='off', left='off', labelleft='off')
plt.box('off')

結果

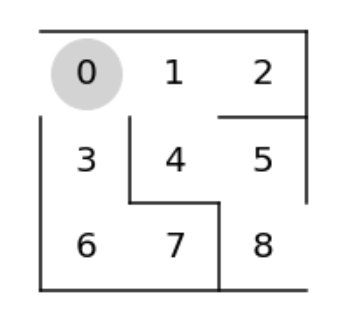
ランダム行動を準備します。
パラメータθと方策を作成し、np.random.choice()でばらつきを加えて作成します。
前回の方策勾配法とは違い、今回パラメータθと方策の更新はありません。

1
2
3
4
5
6
7
8
9
10
# パラメータθの初期値の準備
theta_0 = np.array([
    [np.nan, 1, 1, np.nan], # 0
    [np.nan, 1, 1, 1], # 1
    [np.nan, np.nan, np.nan, 1], # 2
    [1, np.nan, 1, np.nan], # 3
    [1, 1, np.nan, np.nan], # 4
    [np.nan, np.nan, 1, 1], # 5
    [1, 1, np.nan, np.nan], # 6
    [np.nan, np.nan, np.nan, 1]]) # 7

パラメータθから方策のへの変換には単純な割合計算を行います。

1
2
3
4
5
6
7
8
9
# パラメータθを方策に変換
def get_pi(theta):
    # 割合の計算
    [m, n] = theta.shape
    pi = np.zeros((m, n))
    for i in range(0, m):
        pi[i, :] = theta[i, :] / np.nansum(theta[i, :])
    pi = np.nan_to_num(pi)    
    return pi

パラメータθの初期値を変換します。列の合計が１になっています。

1
2
3
# パラメータθの初期値を方策に変換
pi_0 = get_pi(theta_0)
print(pi_0)

結果

行動価値関数を表形式で準備します。
学習前は行動価値関数は不明なので、移動可能が方向は乱数、移動不可の方向は欠損値（np.nan）で初期化します。

1
2
3
4
# 行動価値関数の準備
[a, b] = theta_0.shape
Q = np.random.rand(a, b) * theta_0 * 0.01
print(Q)

結果

行動に従って次の状態を取得する関数を作成します。

1
2
3
4
5
6
7
8
9
10
# 行動に従って次の状態を取得
def get_s_next(s, a):
    if a == 0: # 上
        return s - 3
    elif a == 1: # 右
        return s + 1
    elif a == 2: # 下
        return s + 3
    elif a == 3: # 左
        return s - 1

確率ε(0以上1以下)でランダムに行動し、確率1-εで行動価値関数の行動を選択します。

1
2
3
4
5
6
7
8
# ランダムまたは行動価値関数に従って行動を取得
def get_a(s, Q, epsilon, pi_0):
    if np.random.rand() < epsilon:
        # ランダムに行動を選択
        return np.random.choice([0, 1, 2, 3], p=pi_0[s])
    else:
        # 行動価値関数で行動を選択
        return np.nanargmax(Q[s])

Sarsaの行動価値関数の更新は、パラメータθに学習係数とTD誤差を掛けた値を加算します。

1
2
3
4
5
6
7
8
9
10
# Sarsaによる行動価値関数の更新
def sarsa(s, a, r, s_next, a_next, Q):
    eta = 0.1 # 学習係数
    gamma = 0.9 # 時間割引率
    
    if s_next == 8:
        Q[s, a] = Q[s, a] + eta * (r - Q[s, a])
    else:
        Q[s, a] = Q[s, a] + eta * (r + gamma * Q[s_next, a_next] - Q[s, a])
    return Q

Q-learningの行動価値関数の更新は、次ステップの価値最大の行動を使用します。
（Sarsaと異なりランダム性を含みません）

1
2
3
4
5
6
7
8
9
10
# Q学習による行動価値関数の更新
def q_learning(s, a, r, s_next, a_next, Q):
    eta = 0.1 # 学習係数
    gamma = 0.9 # 時間割引率
    
    if s_next == 8:
        Q[s, a] = Q[s, a] + eta * (r - Q[s, a])
    else:
        Q[s, a] = Q[s, a] + eta * (r + gamma * np.nanmax(Q[s_next, :]) - Q[s, a])
    return Q

１エピソードを実行して履歴と行動価値を取得します。
履歴は[状態, 行動]のリストです。

Sarsaの場合は行動価値関数としてsarsa()を使い、Q-learnigの場合はq-learning()を使います。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
# 1エピソードの実行
def play(Q, epsilon, pi, type):
    s = 0 # 状態
    a = a_next = get_a(s, Q, epsilon, pi) # 行動の初期値
    s_a_history = [[0, np.nan]] # 状態と行動の履歴

    # エピソード完了までループ
    while True:
        # 行動に従って次の状態の取得
        a = a_next
        s_next = get_s_next(s, a)

        # 履歴の更新
        s_a_history[-1][1] = a
        s_a_history.append([s_next, np.nan])

        # 終了判定
        if s_next == 8:
            r = 1
            a_next = np.nan
        else:
            r = 0
            # 行動価値関数Qに従って行動の取得
            a_next = get_a(s_next, Q, epsilon, pi)

        # 行動価値関数の更新
        if type == 1:
            Q = sarsa(s, a, r, s_next, a_next, Q)
        else:
            Q = q_learning(s, a, r, s_next, a_next, Q)

        # 終了判定
        if s_next == 8:
            break
        else:
            s = s_next

    # 履歴と行動価値関数を返す
    return [s_a_history, Q]

エピソードを繰り返し実行して学習を行います。今回は１０回エピソードを実行しています。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
epsilon = 0.5  # ε-greedy法のεの初期値
# 行動価値関数を初期化
Q = np.random.rand(a, b) * theta_0 * 0.01

# エピソードを繰り返し実行して学習
print('=== Sarsa ===')
for episode in range(10):
    # ε-greedyの値を少しずつ小さくする
    epsilon = epsilon / 2

    # 1エピソード実行して履歴と行動価値関数を取得
    [s_a_history, Q] = play(Q, epsilon, pi_0, 1)
    
    # 出力
    print('エピソード: {}, ステップ: {}'.format(
        episode, len(s_a_history)-1))

epsilon = 0.5  # ε-greedy法のεの初期値
# 行動価値関数を初期化
Q = np.random.rand(a, b) * theta_0 * 0.01

# エピソードを繰り返し実行して学習
print('=== Q-learning ===')
for episode in range(10):
    # ε-greedyの値を少しずつ小さくする
    epsilon = epsilon / 2

    # 1エピソード実行して履歴と行動価値関数を取得
    [s_a_history, Q] = play(Q, epsilon, pi_0, 2)
    
    # 出力
    print('エピソード: {}, ステップ: {}'.format(
        episode, len(s_a_history)-1))

SarsaとQ-learningでそれぞれ最短ステップの４に収束していることがわかります。
またSarsaよりQ-learningの方が収束が早いこともわかります。
結果

最後の履歴をもとにアニメーション表示を行ってみます。
（Sarsa、Q-learningともに最終的には同じ結果になります。）

1
2
3
4
5
6
7
8
9
10
# アニメーションの定期処理を行う関数
def animate(i):
    state = s_a_history[i][0]
    circle.set_data((state % 3) + 0.5, 2.5 - int(state / 3))
    return circle

# アニメーションの表示
anim = animation.FuncAnimation(fig, animate, \
        frames=len(s_a_history), interval=1000, repeat=False)
HTML(anim.to_jshtml())

(Google Colaboratoryで動作確認しています。)

参考

AlphaZero 深層学習・強化学習・探索 人工知能プログラミング実践入門 サポートページ