強化学習 AlphaZero 1 (スロットマシーン)

スロットマシーン問題を強化学習で解いていきます。

  • スロットマシーンの目的はコインを多く出すことです。
  • 行動は１回ごとで状態はありません。
  • 行動はどのアームを選択するかであり、報酬はコインが出れば＋１です。
  • 学習方法はε-greedyとUCB1を使います。
  • パラメータの更新間隔は行動１回ごとです。

まずは必要なパッケージをインポートします。

1
2
3
4
5
6
7
# パッケージのインポート
import numpy as np
import random
import math
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline

スロットのアームを表すクラスを作成します。
コンストラクタには「コインが出る確率」を指定します。
draw()でアームを選択したときの報酬を取得します。

1
2
3
4
5
6
7
8
9
10
11
12
# スロットのアームの作成
class SlotArm():
    # スロットのアームの初期化
    def __init__(self, p):
        self.p = p # コインが出る確率

    # アームを選択した時の報酬の取得
    def draw(self):
        if self.p > random.random() :
            return 1.0
        else:
            return 0.0

ε-greedyの計算処理を実装します。
コンストラクタにアームの数を指定し、select_arm()でポリシーに従ってアームを選択します。
その後に、update()で試行回数と価値を更新します。
報酬は、「前回の平均報酬」と「今回の報酬」から平均報酬を算出しています。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
# ε-greedyの計算処理の作成
class EpsilonGreedy():
    # ε-greedyの計算処理の初期化
    def __init__(self, epsilon):
        self.epsilon = epsilon # 探索する確率

    # 試行回数と価値のリセット
    def initialize(self, n_arms):
        self.n = np.zeros(n_arms) # 各アームの試行回数
        self.v = np.zeros(n_arms) # 各アームの価値

    # アームの選択
    def select_arm(self):
        if self.epsilon > random.random():
            # ランダムにアームを選択
            return np.random.randint(0, len(self.v))
        else:
            # 価値が高いアームを選択
            return np.argmax(self.v)

    # アルゴリズムのパラメータの更新
    def update(self, chosen_arm, reward, t):
        # 選択したアームの試行回数に1加算
        self.n[chosen_arm] += 1

        # 選択したアームの価値の更新
        n = self.n[chosen_arm]
        v = self.v[chosen_arm]
        self.v[chosen_arm] = ((n-1) / float(n)) * v + (1 / float(n)) * reward

    # 文字列情報の取得
    def label(self):
        return 'ε-greedy('+str(self.epsilon)+')'

次にUCB1の計算処理を実装します。
初期化(initialize)の引数にアーム数を指定し、select_arm()でポリシーに従ってアームを選択します。
その後に、update()で試行回数と価値を更新します。

UCB1のアルゴリズムのパラメータ更新方法は次の通りです。

  • 成功時は選択したアームの成功回数に１を加算
  • 試行回数が０のアームがあるときは価値を更新しない（0の除算を防ぐため）
  • 各アームの価値の更新（選択されたアームだけではなく全アームの価値が更新される）
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    # UCB1アルゴリズム
    class UCB1():
        # 試行回数と成功回数と価値のリセット
        def initialize(self, n_arms): 
            self.n = np.zeros(n_arms) # 各アームの試行回数
            self.w = np.zeros(n_arms) # 各アームの成功回数
            self.v = np.zeros(n_arms) # 各アームの価値
        
        # アームの選択
        def select_arm(self):
            # nが全て1以上になるようにアームを選択
            for i in range(len(self.n)):
                if self.n[i] == 0:
                    return i
            
            # 価値が高いアームを選択
            return np.argmax(self.v)
            
        # アルゴリズムのパラメータの更新
        def update(self, chosen_arm, reward, ｔ):
            # 選択したアームの試行回数に1加算
            self.n[chosen_arm] += 1

            # 成功時は選択したアームの成功回数に1加算
            if reward == 1.0:
                self.w[chosen_arm] += 1
            
            # 試行回数が0のアームの存在時は価値を更新しない
            for i in range(len(self.n)):
                if self.n[i] == 0:
                    return
            
            # 各アームの価値の更新
            for i in range(len(self.v)):
                self.v[i] = self.w[i] / self.n[i] + (2 * math.log(t) / self.n[i]) ** 0.5
            
        # 文字列情報の取得
        def label(self):
            return 'ucb1'
    シミュレーションを実行(play)します。
  • アームを準備します。（確率は30%、50%、90%とします）
  • アルゴリズムを準備します。（ε-greedyとUCB1を使います。）
  • シミュレーションを実行します。（250回を1セットとして1000セット実行します）
  • グラフを表示します。（DataFrameのgroupby()でグループ化し、mean()で平均報酬を算出します）
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    44
    45
    46
    47
    # シミュレーションの実行
    def play(algo, arms, num_sims, num_time):
        # 履歴の準備
        times = np.zeros(num_sims * num_time) # ゲーム回数の何回目か
        rewards = np.zeros(num_sims * num_time) # 報酬

        # シミュレーション回数分ループ
        for sim in range(num_sims):
            algo.initialize(len(arms)) # アルゴリズム設定の初期化

            # ゲーム回数分ループ
            for time in range(num_time):
                # インデックスの計算
                index = sim * num_time + time

                # 履歴の計算
                times[index] = time+1
                chosen_arm = algo.select_arm()
                reward = arms[chosen_arm].draw()
                rewards[index] = reward

                # アルゴリズムのパラメータの更新
                algo.update(chosen_arm, reward, time+1)

        # [ゲーム回数の何回目か, 報酬]
        return [times, rewards]

    # アームの準備
    arms = (SlotArm(0.3), SlotArm(0.5), SlotArm(0.9))

    # アルゴリズムの準備
    algos = (EpsilonGreedy(0.1),  UCB1())

    for algo in algos:
        # シミュレーションの実行
        results = play(algo, arms, 1000, 250)
        
        # グラフの表示
        df = pd.DataFrame({'times': results[0], 'rewards': results[1]})
        mean = df['rewards'].groupby(df['times']).mean()
        plt.plot(mean, label=algo.label()) 

    # グラフの表示
    plt.xlabel('Step')
    plt.ylabel('Average Reward')
    plt.legend(loc='best')
    plt.show()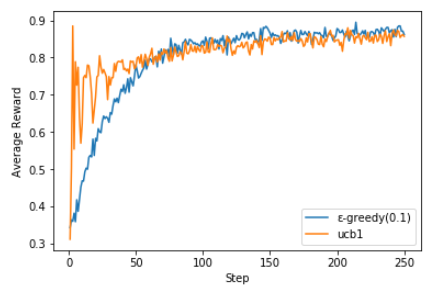
    結果は下記の通りです。
    結果
    UCB1の方がゲーム最初から報酬が高いですが、最終的には両方とも安定した結果になっていることが分かります。

(Google Colaboratoryで動作確認しています。)

参考

AlphaZero 深層学習・強化学習・探索 人工知能プログラミング実践入門 サポートページ