強化学習6 (TD法)

前回は１エピソードをプレイした実績に基づく更新を行うモンテカルロ法による学習を試してみました。
今回は１回の行動ごとに更新を行うTD法と試してみます。

モンテカルロ法に比べて行動修正のスピードが早いため学習が効率的です。
ただ更新は見積りベースになるためモンテカルロ法より適切な行動をとれるかどうか不確実になります。

まずはエージェントのベースになるクラスを実装します。(強化学習5 (モンテカルロ法)と同様です。)

el_agent.py
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
import numpy as np
import matplotlib.pyplot as plt

class ELAgent():

    def __init__(self, epsilon):
        self.Q = {}
        self.epsilon = epsilon
        self.reward_log = []

    def policy(self, s, actions):
        if np.random.random() < self.epsilon:
            # ランダムな行動（探索）
            return np.random.randint(len(actions))
        else:
            # self.Q => 状態における行動の価値
            # self.Q[s] => 状態sで行動aをとる場合の価値
            if s in self.Q and sum(self.Q[s]) != 0:
                # 価値評価に基づき行動（活用）
                return np.argmax(self.Q[s])
            else:
                # ランダムな行動（探索）
                return np.random.randint(len(actions))

    # 報酬の記録を初期化
    def init_log(self):
        self.reward_log = []

    # 報酬の記録
    def log(self, reward):
        self.reward_log.append(reward)

    def show_reward_log(self, interval=50, episode=-1):
        # そのepsilonの報酬をグラフ表示
        if episode > 0:
            rewards = self.reward_log[-interval:]
            mean = np.round(np.mean(rewards), 3)
            std = np.round(np.std(rewards), 3)
            print("At Episode {} average reward is {} (+/-{}).".format(
                   episode, mean, std))
        # 今までに獲得した報酬をグラフ表示
        else:
            indices = list(range(0, len(self.reward_log), interval))
            means = []
            stds = []
            for i in indices:
                rewards = self.reward_log[i:(i + interval)]
                means.append(np.mean(rewards))
                stds.append(np.std(rewards))
            means = np.array(means)
            stds = np.array(stds)
            plt.figure()
            plt.title("Reward History")
            plt.grid()
            plt.fill_between(indices, means - stds, means + stds,
                             alpha=0.1, color="g")
            plt.plot(indices, means, "o-", color="g",
                     label="Rewards for each {} episode".format(interval))
            plt.legend(loc="best")
            plt.show()

次に環境を扱うためのクラスを実装します。

FrozenLakeEasy-v0は、強化学習を行うための環境を提供するライブラリOpenAI Gymの環境の１つです。
4 x 4 マスの迷路でところどころに穴があいていて穴に落ちるとゲーム終了となります。
穴に落ちずにゴールに到着すると報酬が得られます。(強化学習5 (モンテカルロ法)と同様です。)

frozen_lake_util.py
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.cm as cm
import gym
from gym.envs.registration import register
# スリップする設定(is_slippery)をオフ設定（学習に時間がかかるため）
register(id="FrozenLakeEasy-v0", entry_point="gym.envs.toy_text:FrozenLakeEnv", kwargs={"is_slippery": False})

def show_q_value(Q):
    """
    FrozenLake-v0環境での価値は下記の通り。
    各行動での評価を表しています。
    +----+------+----+
    |    |  上  |    |
    | 左 | 平均 | 右 |
    |    |  下  |    |
   +-----+------+----+
    """
    env = gym.make("FrozenLake-v0")
    nrow = env.unwrapped.nrow
    ncol = env.unwrapped.ncol
    state_size = 3
    q_nrow = nrow * state_size
    q_ncol = ncol * state_size
    reward_map = np.zeros((q_nrow, q_ncol))

    for r in range(nrow):
        for c in range(ncol):
            s = r * nrow + c
            state_exist = False
            if isinstance(Q, dict) and s in Q:
                state_exist = True
            elif isinstance(Q, (np.ndarray, np.generic)) and s < Q.shape[0]:
                state_exist = True

            if state_exist:
                # At the display map, the vertical index is reversed.
                _r = 1 + (nrow - 1 - r) * state_size
                _c = 1 + c * state_size
                reward_map[_r][_c - 1] = Q[s][0]  # 左 = 0
                reward_map[_r - 1][_c] = Q[s][1]  # 下 = 1
                reward_map[_r][_c + 1] = Q[s][2]  # 右 = 2
                reward_map[_r + 1][_c] = Q[s][3]  # 上 = 3
                reward_map[_r][_c] = np.mean(Q[s])  # 中央

    # 各状態・行動の評価を表示
    fig = plt.figure()
    ax = fig.add_subplot(1, 1, 1)
    plt.imshow(reward_map, cmap=cm.RdYlGn, interpolation="bilinear",
               vmax=abs(reward_map).max(), vmin=-abs(reward_map).max())
    # 報酬推移を表示
    ax.set_xlim(-0.5, q_ncol - 0.5)
    ax.set_ylim(-0.5, q_nrow - 0.5)
    ax.set_xticks(np.arange(-0.5, q_ncol, state_size))
    ax.set_yticks(np.arange(-0.5, q_nrow, state_size))
    ax.set_xticklabels(range(ncol + 1))
    ax.set_yticklabels(range(nrow + 1))
    ax.grid(which="both")
    plt.show()

TD法での学習を実行します。
(このファイルだけ強化学習5 (モンテカルロ法)と異なります。)

q_learning.py
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
from collections import defaultdict
import gym
from el_agent import ELAgent
from frozen_lake_util import show_q_value

class QLearningAgent(ELAgent):

    def __init__(self, epsilon=0.1):
        super().__init__(epsilon)

    def learn(self, env, episode_count=1000, gamma=0.9,
              learning_rate=0.1, render=False, report_interval=50):
        self.init_log()
        actions = list(range(env.action_space.n)) # actions = [0, 1, 2, 3]
        # self.Q Qテーブル(ある状態sにおける行動aの報酬を管理)
        self.Q = defaultdict(lambda: [0] * len(actions))
        for e in range(episode_count):
            s = env.reset()
            done = False
            while not done:
                if render:
                    env.render()
                a = self.policy(s, actions)
                n_state, reward, done, info = env.step(a)

                # reward => 報酬
                # gamma => 割引率
                # max(self.Q[n_state]) => 価値が最大になるような行動をとる
                gain = reward + gamma * max(self.Q[n_state])
                estimated = self.Q[s][a]
                # Qテーブルの更新(状態sの行動aにおける報酬を管理)
                #   learning_rate => 学習率
                #   estimated => 既存の見積り
                self.Q[s][a] += learning_rate * (gain - estimated)
                s = n_state
            else:
                self.log(reward)

            if e != 0 and e % report_interval == 0:
                self.show_reward_log(episode=e)

# 学習を行う
def train():
    agent = QLearningAgent()
    env = gym.make("FrozenLakeEasy-v0")
    agent.learn(env, episode_count=500)
    show_q_value(agent.Q)
    agent.show_reward_log()

if __name__ == "__main__":
    train()
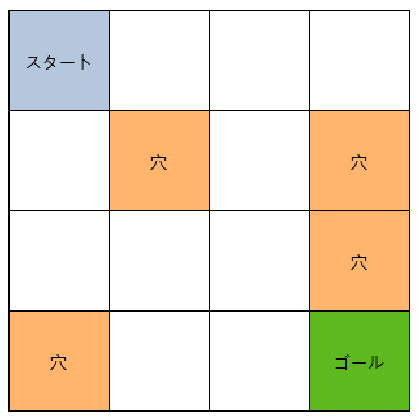
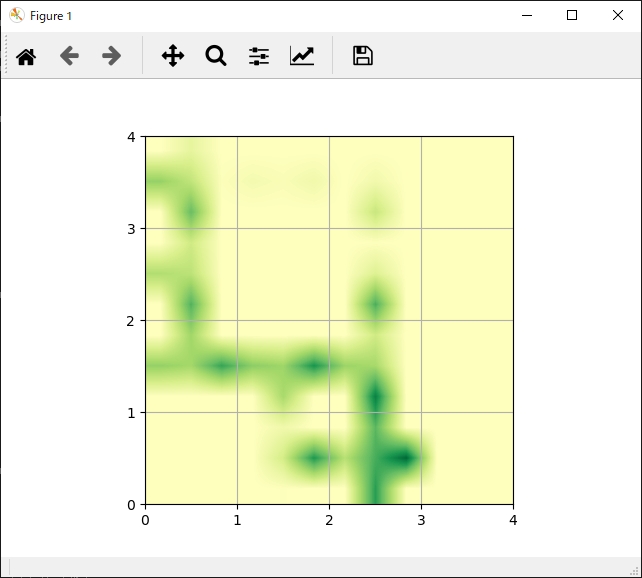
FrozenLake 各行動の評価

全体的にゴール向かう行動が高く評価されていることがわかります。

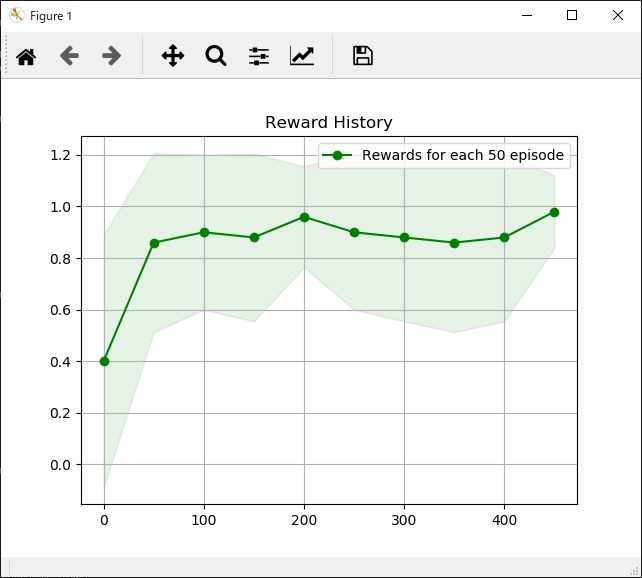
エピソード実行回数と獲得報酬平均の推移は次のようになります。
エピソード数と獲得報酬平均の推移

モンテカルロ法と同様にうまく学習できています。

参考

Pythonで学ぶ強化学習 -入門から実践まで- サンプルコード