強化学習5 (モンテカルロ法)

モンテカルロ法は行動の修正を実績に基づき行う方法です。
エピソードが終了した後で、獲得できた報酬の総和をもとに修正を行うシンプルな方法です。

まずはエージェントのベースになるクラスを実装します。

el_agent.py
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
import numpy as np
import matplotlib.pyplot as plt

class ELAgent():

    def __init__(self, epsilon):
        self.Q = {}
        self.epsilon = epsilon
        self.reward_log = []

    def policy(self, s, actions):
        if np.random.random() < self.epsilon:
            # ランダムな行動（探索）
            return np.random.randint(len(actions))
        else:
            # self.Q => 状態における行動の価値
            # self.Q[s] => 状態sで行動aをとる場合の価値
            if s in self.Q and sum(self.Q[s]) != 0:
                # 価値評価に基づき行動（活用）
                return np.argmax(self.Q[s])
            else:
                # ランダムな行動（探索）
                return np.random.randint(len(actions))

    # 報酬の記録を初期化
    def init_log(self):
        self.reward_log = []

    # 報酬の記録
    def log(self, reward):
        self.reward_log.append(reward)

    def show_reward_log(self, interval=50, episode=-1):
        # そのepsilonの報酬をグラフ表示
        if episode > 0:
            rewards = self.reward_log[-interval:]
            mean = np.round(np.mean(rewards), 3)
            std = np.round(np.std(rewards), 3)
            print("At Episode {} average reward is {} (+/-{}).".format(
                   episode, mean, std))
        # 今までに獲得した報酬をグラフ表示
        else:
            indices = list(range(0, len(self.reward_log), interval))
            means = []
            stds = []
            for i in indices:
                rewards = self.reward_log[i:(i + interval)]
                means.append(np.mean(rewards))
                stds.append(np.std(rewards))
            means = np.array(means)
            stds = np.array(stds)
            plt.figure()
            plt.title("Reward History")
            plt.grid()
            plt.fill_between(indices, means - stds, means + stds,
                             alpha=0.1, color="g")
            plt.plot(indices, means, "o-", color="g",
                     label="Rewards for each {} episode".format(interval))
            plt.legend(loc="best")
            plt.show()

次に環境を扱うためのクラスを実装します。

FrozenLakeEasy-v0は、強化学習を行うための環境を提供するライブラリOpenAI Gymの環境の１つです。
4 x 4 マスの迷路でところどころに穴があいていて穴に落ちるとゲーム終了となります。
穴に落ちずにゴールに到着すると報酬が得られます。

frozen_lake_util.py
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.cm as cm
import gym
from gym.envs.registration import register
# スリップする設定(is_slippery)をオフ設定（学習に時間がかかるため）
register(id="FrozenLakeEasy-v0", entry_point="gym.envs.toy_text:FrozenLakeEnv", kwargs={"is_slippery": False})

def show_q_value(Q):
    """
    FrozenLake-v0環境での価値は下記の通り。
    各行動での評価を表しています。
    +----+------+----+
    |    |  上  |    |
    | 左 | 平均 | 右 |
    |    |  下  |    |
   +-----+------+----+
    """
    env = gym.make("FrozenLake-v0")
    nrow = env.unwrapped.nrow
    ncol = env.unwrapped.ncol
    state_size = 3
    q_nrow = nrow * state_size
    q_ncol = ncol * state_size
    reward_map = np.zeros((q_nrow, q_ncol))

    for r in range(nrow):
        for c in range(ncol):
            s = r * nrow + c
            state_exist = False
            if isinstance(Q, dict) and s in Q:
                state_exist = True
            elif isinstance(Q, (np.ndarray, np.generic)) and s < Q.shape[0]:
                state_exist = True

            if state_exist:
                # At the display map, the vertical index is reversed.
                _r = 1 + (nrow - 1 - r) * state_size
                _c = 1 + c * state_size
                reward_map[_r][_c - 1] = Q[s][0]  # 左 = 0
                reward_map[_r - 1][_c] = Q[s][1]  # 下 = 1
                reward_map[_r][_c + 1] = Q[s][2]  # 右 = 2
                reward_map[_r + 1][_c] = Q[s][3]  # 上 = 3
                reward_map[_r][_c] = np.mean(Q[s])  # 中央

    # 各状態・行動の評価を表示
    fig = plt.figure()
    ax = fig.add_subplot(1, 1, 1)
    plt.imshow(reward_map, cmap=cm.RdYlGn, interpolation="bilinear",
               vmax=abs(reward_map).max(), vmin=-abs(reward_map).max())
    # 報酬推移を表示
    ax.set_xlim(-0.5, q_ncol - 0.5)
    ax.set_ylim(-0.5, q_nrow - 0.5)
    ax.set_xticks(np.arange(-0.5, q_ncol, state_size))
    ax.set_yticks(np.arange(-0.5, q_nrow, state_size))
    ax.set_xticklabels(range(ncol + 1))
    ax.set_yticklabels(range(nrow + 1))
    ax.grid(which="both")
    plt.show()

モンテカルロ法での学習を実行します。

monte_carlo.py
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
import math
from collections import defaultdict
import gym
from el_agent import ELAgent
from frozen_lake_util import show_q_value

class MonteCarloAgent(ELAgent):

    def __init__(self, epsilon=0.1):
        super().__init__(epsilon)

    def learn(self, env, episode_count=1000, gamma=0.9,
              render=False, report_interval=50):
        self.init_log()
        actions = list(range(env.action_space.n))
        self.Q = defaultdict(lambda: [0] * len(actions))
        N = defaultdict(lambda: [0] * len(actions))

        for e in range(episode_count):
            s = env.reset()
            done = False
            # エピソードの終了まで実行する
            experience = []
            while not done:
                if render:
                    env.render()
                a = self.policy(s, actions)
                n_state, reward, done, info = env.step(a)
                experience.append({"state": s, "action": a, "reward": reward})
                s = n_state
            else:
                self.log(reward)

            # 各状態・各行動を評価する。
            for i, x in enumerate(experience):
                s, a = x["state"], x["action"]

                # Calculate discounted future reward of s.
                # 状態ｓ
                G, t = 0, 0
                for j in range(i, len(experience)):
                    G += math.pow(gamma, t) * experience[j]["reward"]
                    t += 1

                N[s][a] += 1  # count of s, a pair
                alpha = 1 / N[s][a]
                self.Q[s][a] += alpha * (G - self.Q[s][a])

            if e != 0 and e % report_interval == 0:
                self.show_reward_log(episode=e)

def train():
    agent = MonteCarloAgent(epsilon=0.1)
    env = gym.make("FrozenLakeEasy-v0")
    agent.learn(env, episode_count=500)
    show_q_value(agent.Q)
    agent.show_reward_log()

if __name__ == "__main__":
    train()

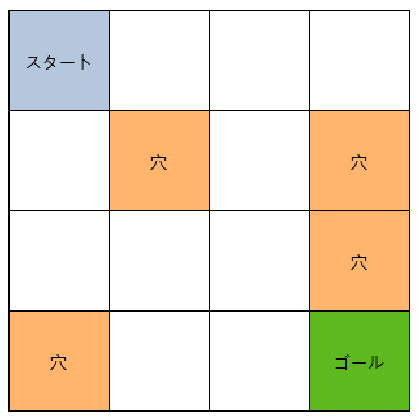
FrozenLakeの設定と各行動の評価結果は下記のようになります。
緑色が濃いほど評価が高いことを意味します。

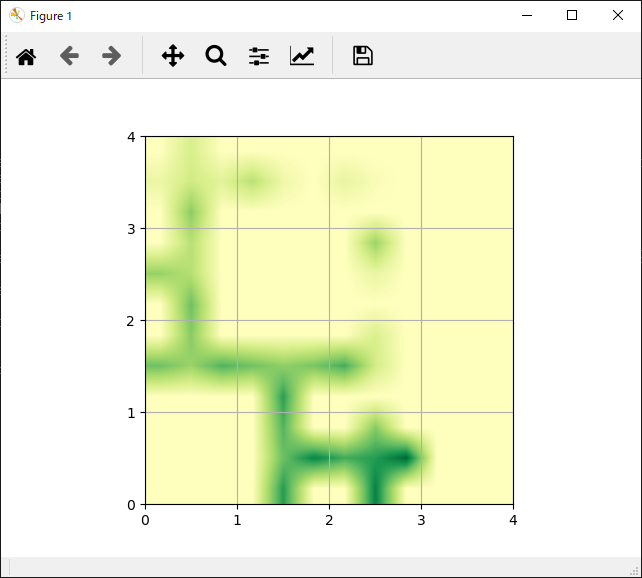
FrozenLake 各行動の評価

全体的にゴール向かう行動が高く評価されていることがわかります。

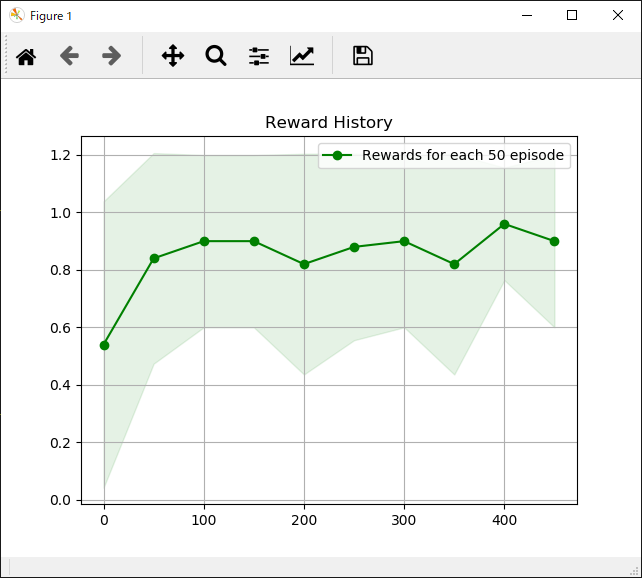
エピソード実行回数と獲得報酬平均の推移は次のようになります。
エピソード数と獲得報酬平均の推移
エピソード実行が50回付近で報酬が1近くに達していて学習がだいたい完了していることがわかります。

参考

Pythonで学ぶ強化学習 -入門から実践まで- サンプルコード