強化学習4 (経験から計画を立てる)

遷移関数や報酬関数が分からない場合は、行動してみて状態の遷移や得られる報酬を調べていくことになります。
今回は、Epsilon-Greedy法で探索（経験を蓄積する）と活用（行動する）の割合によって報酬がどのように変わっていくかを調査します。

何枚かのコインから１枚を選んで、投げた時に表がでれば報酬が得られるゲームで実装しています。
以下がコードになります。（コメントにて処理を確認して頂ければ幸いです）

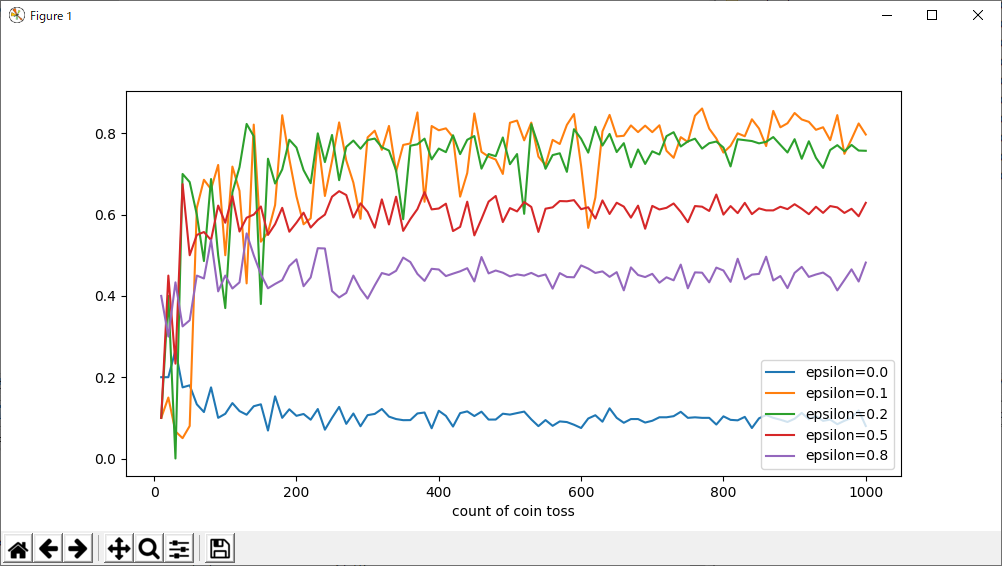
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
import random
import numpy as np


class CoinToss():

    # head_probsは各コインの表が出る確率
    def __init__(self, head_probs, max_episode_steps=30):
        self.head_probs = head_probs
        self.max_episode_steps = max_episode_steps
        self.toss_count = 0

    def __len__(self):
        return len(self.head_probs)

    def reset(self):
        self.toss_count = 0

    # actionはコインのindex
    def step(self, action):
        # max_episode_stepsはデフォルト30回
        final = self.max_episode_steps - 1
        if self.toss_count > final:
            raise Exception("The step count exceeded maximum. Please reset env.")
        else:
            # 終了確認
            done = True if self.toss_count == final else False

        if action >= len(self.head_probs):
            raise Exception("The No.{} coin doesn't exist.".format(action))
        else:
            head_prob = self.head_probs[action]
            if random.random() < head_prob:
                reward = 1.0
            else:
                reward = 0.0
            self.toss_count += 1
            return reward, done


class EpsilonGreedyAgent():

    def __init__(self, epsilon):
        self.epsilon = epsilon
        self.V = []

    def policy(self):
        coins = range(len(self.V))
        # random関数は0.0から1.0の値を返す。
        if random.random() < self.epsilon:
            # 活用優先（行動する）
            return random.choice(coins) # コインのindexをランダムに返す
        else:
            # 探索優先(経験を蓄積)
            return np.argmax(self.V)  # 配列中の最大値のindexを返す

    def play(self, env):
        # 初期化
        # len(env)はコインごとの表がでる確率の配列
        N = [0] * len(env)       # [0, 0, 0, 0, ・・・]という配列ができる
        self.V = [0] * len(env)

        env.reset()
        done = False
        rewards = []
        while not done:
            # ランダムに選ばれたコインか、平均報酬が一番高いコインが返る
            selected_coin = self.policy()
            reward, done = env.step(selected_coin)
            rewards.append(reward)

            n = N[selected_coin]
            coin_average = self.V[selected_coin]
            new_average = (coin_average * n + reward) / (n + 1)
            N[selected_coin] += 1
            # そのコインの平均報酬
            self.V[selected_coin] = new_average
        # 全ての報酬を配列で返す
        return rewards

if __name__ == "__main__":
    import pandas as pd
    import matplotlib.pyplot as plt

    def main():
        env = CoinToss([0.1, 0.5, 0.1, 0.9, 0.1])      # 各コインの表がでる確率
        # 探索優先(0.0に近いほど)か活用優先(1.0に近いほど)かの割合
        epsilons = [0.0, 0.1, 0.2, 0.5, 0.8]
        game_steps = list(range(10, 1010, 10))  # 10回から1000回まで10回おきに実行する
        result = {}
        for e in epsilons:
            agent = EpsilonGreedyAgent(epsilon=e)
            means = []
            for s in game_steps:
                env.max_episode_steps = s
                rewards = agent.play(env)
                means.append(np.mean(rewards))
            result["epsilon={}".format(e)] = means
        result["count of coin toss"] = game_steps
        result = pd.DataFrame(result)
        result.set_index("count of coin toss", drop=True, inplace=True)
        result.plot.line(figsize=(10, 5))
        plt.show()

    main()

結果
epsilonが0.0の場合はコイントスの回数を増やしても報酬がぜんぜん増えていません。
epsilonが0.1か0.2くらいだといい結果がでています。
一般的にepsilonは0.1に設定することが多いようですが、今回の結果はそれを裏付けることとなりました。