ニューラルネットワーク(2)

学習メソッドtrainを実装します。前回実装した照会メソッドqueryと似ています。
重みをかけて発火させたあとに目標出力との誤差を算出しそれを学習率に応じて重みに反映する・・・これがニューラルネットワークの最重要ポイントかと思われます。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
import numpy
import scipy.special

class neural_network:
    # 【初期化】
    # 入力層、隠れ層、出力層のノード数を設定する。
    def __init__(self, in_node, hid_node, out_node, learn_rate):
        self.in_node = in_node       # 入力層
        self.hid_node = hid_node     # 隠れ層
        self.out_node = out_node     # 出力層
        self.learn_rate = learn_rate # 学習率
        
        # 重み行列（処理の核となる）
        # 正規分布の平均、標準偏差、配列の大きさを設定
        self.weight_in_hid  = numpy.random.normal(0.0, pow(self.hid_node, -0.5), (self.hid_node, self.in_node))
        ''' ↓こんな感じの配列ができる
        [[ 0.37395332  0.07296579  0.36696637]
         [-0.1570748   0.28908756  0.99958053]
         [-0.09054778 -0.20084478  0.31981826]]
        '''
        self.weight_hid_out = numpy.random.normal(0.0, pow(self.out_node, -0.5), (self.out_node, self.hid_node))
        ''' ↓こんな感じの配列ができる
        [[ 0.93304259  0.02641947  0.29506316]
         [-0.74275445  0.9010841  -0.47840667]
         [ 0.04494529  0.49177323  1.13985481]]
         '''
        
        # 活性化関数はシグモイド関数
        self.activation_func = lambda x: scipy.special.expit(x)

    # 【学習】
    #  学習データから重みを調整する。
    def train(self, in_list, target_list):
        # 入力データ（１次元）を２次元化して転置をとる。
        #（横長の配列が縦長になる）
        in_matrix = numpy.array(in_list, ndmin=2).T
        target_matrix = numpy.array(target_list, ndmin=2).T
        # -------------- 重みをかけて発火させる -------------- 
        # 入力層→隠れ層の計算
        hid_in = numpy.dot(self.weight_in_hid, in_matrix)
        hid_out = self.activation_func(hid_in)
        
        # 隠れ層→出力層の計算
        final_in = numpy.dot(self.weight_hid_out, hid_out)
        final_out = self.activation_func(final_in)
        # -------------- 誤差の計算 -------------- 
        # 出力層の誤差（目標出力 - 最終出力）
        out_err = target_matrix - final_out
        # 隠れ層の誤差は出力層の誤差をリンクの重みの割合で分配
        hid_err = numpy.dot(self.weight_hid_out.T, out_err)
        # -------------- 重みの更新（処理の核） -------------- 
        # 隠れ層と出力層の間のリンクの重みを更新
        self.weight_hid_out += self.learn_rate * numpy.dot((out_err * final_out * (1.0 - final_out)), numpy.transpose(hid_out))
        
        # 入力層と隠れ層の間のリンクの重みを更新
        self.weight_in_hid += self.learn_rate * numpy.dot((hid_err * hid_out * (1.0 - hid_out)), numpy.transpose(in_matrix))
        
    # 【照会】
    # 入力に対して出力層からの答えを返す。
    def query(self, input_list):
        # 入力リストを行列に変換
        # １次元配列は２次元配列に変換し転置をとる。
        #（横長の配列が縦長になる）
        in_matrix = numpy.array(input_list, ndmin=2).T
        
        # 隠れ層に入ってくる信号の計算（入力層に重みをかける）
        hid_in = numpy.dot(self.weight_in_hid, in_matrix)
        # 隠れ層で結合された信号を活性化関数（シグモイド関数）により出力
        # （閾値を超えたものが発火する）
        hid_out = self.activation_func(hid_in)
    
        # 出力層に入ってくる信号の計算（隠れ層に重みをかける）
        final_in = numpy.dot(self.weight_hid_out, hid_out)
        # 出力層で結合された信号を活性化関数（シグモイド関数）により出力
        # （閾値を超えたものが発火する）
        final_out = self.activation_func(final_in)
        
        return final_out

これで自作ニューラルネットワークが完成しました。
このクラスを使ってMNISTデータの判定を行ってみます。

まず、学習データ（１００種類）とテストデータ（１０種類）をダウンロードします。

1
2
!wget https://raw.githubusercontent.com/makeyourownneuralnetwork/makeyourownneuralnetwork/master/mnist_dataset/mnist_test_10.csv
!wget https://raw.githubusercontent.com/makeyourownneuralnetwork/makeyourownneuralnetwork/master/mnist_dataset/mnist_train_100.csv</pre>

データを読み込んで、どんなデータか表示してみます。

1
2
3
4
5
6
7
8
9
10
import numpy
import matplotlib.pyplot
%matplotlib inline

with open('mnist_train_100.csv', 'r') as f:
    data_list = f.readlines()

val = data_list[7].split(',')   # データを選ぶ(0-99の間)
img = numpy.asfarray(val[1:]).reshape((28, 28))
matplotlib.pyplot.imshow(img, cmap='Greys', interpolation='None')

結果

データを学習し、テストデータの１つを選んでどの数字と合致する確率が高いかを表示します。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
import numpy
import matplotlib.pyplot
%matplotlib inline

in_node = 784      # 入力層のノード数(28 * 28)
hid_node = 200     # 隠れ層のノード数
out_node = 10      # 出力層のノード数(0～9を表す)

learn_rate = 0.2  # 学習率

# ニューラルネットワークのインスタンス生成
n_network = neural_network(in_node, hid_node, out_node, learn_rate)

# 学習データファイルを読み込んでリスト化
with open('mnist_train_100.csv', 'r') as f:
    train_data = f.readlines()

# 全学習データを１０回学習
epochs = 10    # 学習回数
for e in range(epochs):
    # 学習データすべてに対して実行
    for record in train_data:
        val = record.split(',')
        # 入力値のスケールとシフト
        in_data = (numpy.asfarray(val[1:]) / 255.0 * 0.99) + 0.01
        # 目標配列の生成（ラベル位置0.99、残り0.01）
        target = numpy.zeros(out_node) + 0.01
        target[int(val[0])] = 0.99
        n_network.train(in_data, target)

# テストデータファイルを読み込んでリスト化
with open('mnist_test_10.csv', 'r') as f:
    test_data = f.readlines()

val = test_data[0].split(',')   # テストデータを選択(0-9の間)
img = numpy.asfarray(val[1:]).reshape((28, 28))
matplotlib.pyplot.imshow(img, cmap='Greys', interpolation='None')

# 選択したデータをニューラルネットワークで照会
res = n_network.query((numpy.asfarray(val[1:]) / 255.0 * 0.99) + 0.01)
for a,b in enumerate(res):
    print('{}の可能性 {:5.2f}%'.format(a,b[0] * 100))

結果

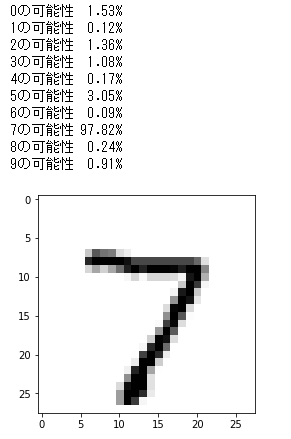
今回は[7]の合致率が97%以上ときちんと認識しているようです。
１０種類あるテストデータをすべて試してみましたが、なかなかよい結果がでてました。
ただ人間でもよくわからないデータ（手書き数字）だとはっきり認識するのは難しいようです。（あたり前か・・・）

隠れ層のノード数、学習率、学習回数の範囲をいろいろ試してみて認識率がどうかわるかを試すのもよいかと思います。

(Google Colaboratoryで動作確認しています。)