グラフ理論 NetworkX

NetworkX

NetworkXは、グラフ理論を用いた問題を解決するためのPythonライブラリです。

以下に、NetworkXで解決できる問題の例です。

🔹グラフの構築や可視化
🔹グラフの特徴量の計算（次数中心性、媒介中心性、近接中心性など）
🔹グラフの操作（ノードやエッジの追加・削除、グラフのサブグラフの抽出など）
🔹最短経路や最短距離の計算
🔹ネットワーク分析や社会ネットワーク分析の実行
🔹グラフの可視化やレイアウトの設定

これらの機能を使って、例えば以下のような問題を解決することができます。

🔹ソーシャルメディアのネットワーク分析による、情報拡散や影響力の分析
🔹輸送網や交通網の最適ルートの検索や交通量の分析
🔹電力網や水道網の効率的な運営のためのネットワーク解析
🔹化学反応のシミュレーションや、生物学的ネットワークの解析
🔹ウェブページのリンク構造の解析や、検索エンジンのランキングアルゴリズムの開発

なお、これらはあくまでも一例であり、グラフ理論が応用される領域は多岐に渡ります。

最短経路問題

最短経路問題とは、あるグラフ上で2つの頂点間の最短経路を求める問題です。

NetworkXライブラリには、最短経路を求めるための関数が用意されています。

以下は、最短経路を求める例として、グラフ上の2つの頂点の最短経路を求めるコードです。

[Google Colaboratory]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
import networkx as nx
import matplotlib.pyplot as plt

# グラフの定義
G = nx.Graph()
G.add_edge(0, 1, weight=4)
G.add_edge(0, 2, weight=3)
G.add_edge(1, 3, weight=2)
G.add_edge(2, 3, weight=5)
G.add_edge(2, 4, weight=6)
G.add_edge(3, 4, weight=1)

# 最短経路の計算
shortest_path = nx.shortest_path(G, source=0, target=4, weight='weight')

# 結果の表示
print(f"The shortest path from node 0 to node 4 is: {shortest_path}")

# グラフの可視化
pos = nx.spring_layout(G)
nx.draw_networkx_nodes(G, pos, node_color='lightblue')
nx.draw_networkx_edges(G, pos)
nx.draw_networkx_labels(G, pos)
edge_labels = {(u, v): d['weight'] for u, v, d in G.edges(data=True)}
nx.draw_networkx_edge_labels(G, pos, edge_labels=edge_labels)
plt.axis('off')
plt.show()

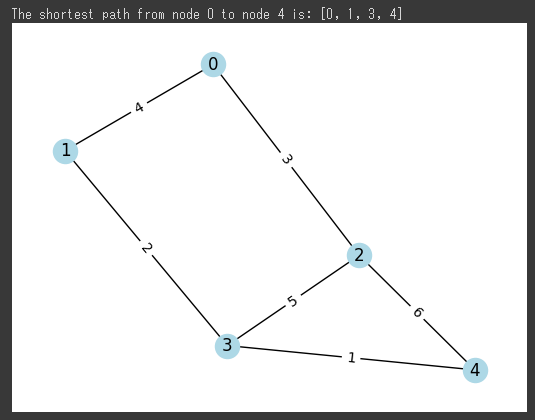
この例では、グラフGを定義して、nx.shortest_path()関数を使って、頂点0から頂点4までの最短経路を計算しています。

nx.shortest_path()関数は、グラフと、最短経路の始点と終点を指定する引数を取り、最短経路を表す頂点のリストを返します。

次に、計算結果を表示し、最後にグラフを可視化しています。

グラフの可視化には、matplotlibライブラリを使用しています。

nx.spring_layout()関数は、グラフのレイアウトを計算する関数であり、nx.draw_networkx_nodes()、nx.draw_networkx_edges()、nx.draw_networkx_labels()、nx.draw_networkx_edge_labels()関数は、それぞれ、ノード、エッジ、ラベル、エッジラベルを描画するための関数です。

[実行結果]