ベルマンフォード法（最短経路問題）

ベルマンフォード法

ベルマンフォード法 は、最短経路問題 を解くアルゴリズムの１つです。

ベルマンフォード法 には次のような特徴があります。

  • 頂点を結んだ 辺の重み（コスト）を更新しながら最短経路を求めます。
  • 辺の重み（コスト）が マイナス の場合でも解くことができます。

次のようなグラフを考えてみます。

[グラフ]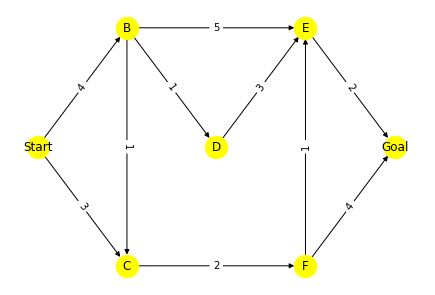

各頂点におけるスタート地点からのコストを求めるにあたり、設定した初期値から辺の重みを使って順に更新する作業を繰り返し、それ以上更新できなくなったら処理を終了します。

ソースコード

ソースコードでは、グラフの情報を次の入力例のように定義してみます。

  • 頂点は名前（頂点名）をもち、それぞれの頂点は隣の頂点情報(edge)と自分のコスト(cost)情報を持っています。
  • 隣の頂点情報は、頂点名（辞書型データのキー）とそこに移動するためのコスト（辞書型データのバリュー）があり、複数存在することがあります。
  • 頂点自体がもっているコストは、そこに辿りつくためのコストであり、初期値としてはスタート地点が０、それ以外は無限大を設定しておきます。

ベルマンフォード法 では、次のような手順で頂点のコスト情報を更新していきます。

  1. 辺を１つ選ぶ。
  2. 選んだ辺のコストを使って、両端の頂点のコストを更新する。
    （コストが小さい頂点に辺のコストを加算した値が、もう一方の頂点のコストよりも小さい場合、更新する）
  3. 全ての頂点に対して、コストが更新されなくなるまで上記の1～2を繰り返す。

[Google Colaboratory]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
#---------- 入力例 ----------
nodes = {                                   # ノード情報
    'Start':{'edge':{'B':4, 'C':3},         # 隣の頂点までのコスト（頂点名:コスト）
             'cost':0},                     # 頂点Startまでの最小コスト
    'B':    {'edge':{'C':1, 'D':1, 'E':5},  # 隣の頂点までのコスト（頂点名:コスト）
             'cost':float('inf')},          # 頂点Bまでの最小コスト
    'C':    {'edge':{'F':2},                # 隣の頂点までのコスト（頂点名:コスト）
             'cost':float('inf')},          # 頂点Cまでの最小コスト
    'D':    {'edge':{'E':3},                # 隣の頂点までのコスト（頂点名:コスト）
             'cost':float('inf')},          # 頂点Dまでの最小コスト
    'E':    {'edge':{'Goal':2},             # 隣の頂点までのコスト（頂点名:コスト）
             'cost':float('inf')},          # 頂点Eまでの最小コスト
    'F':    {'edge':{'E':1, 'Goal':4},      # 隣の頂点までのコスト（頂点名:コスト）
             'cost':float('inf')},          # 頂点Fまでの最小コスト
    'Goal': {'edge':{},                     # 隣の頂点までのコスト（頂点名:コスト）
             'cost':float('inf')}           # 頂点Goalまでの最小コスト
}
#----------------------------
# ベルマンフォード法（辺の重みに注目する方法）
is_updated = True                           # 更新フラグを立てる
while is_updated:                           # 頂点が更新されなくなるまで実行
    is_updated = False                      # 更新フラグを落とす
    for src, node_info in nodes.items():    # 頂点をすべてチェック
        for dst, cost in node_info['edge'].items():             # その頂点からの辺をすべてチェック
            if nodes[src]['cost'] + cost < nodes[dst]['cost']:  # 頂点のコスト＋辺のコストが、次の頂点のコストより小さい場合
                nodes[dst]['cost'] = nodes[src]['cost'] + cost  # 次の頂点のコストを更新
                is_updated = True                               # 更新フラグをたてる
print('解：最小コストは', nodes['Goal']['cost'])

[実行結果]

解：最小コストは 8

頂点Start から 頂点Goal までの最小コストは 8 であることを導き出すことができました。

ベルマンフォード法の注意点

辺のコスト というのは 時間 や 料金、距離 などが対応すると考えられます。

これらはいずれもプラスの値ですが、もしマイナスの値であってもベルマンフォード法は有効です。

ただし、マイナスの値でループ しているような 経路（閉路） がある場合は、そのループを回り続けるといくらでもコストが小さくなってしまうため ベルマンフォード法 では解くことができません。