分類モデルの評価②（適合率／再現率／F1値）

適合率

適合モデルは、モデルがどれだけ正確に予測できいるかを示す指標です。

適合率の算出には、precision_scoreを使用します。

[Google Colaboratory]

1
2
3
4
from sklearn.metrics import precision_score

print(f"訓練データ適合率：{precision_score(y_train,y_train_pred,pos_label=0)}")
print(f"テストデータ適合率：{precision_score(y_test,y_test_pred,pos_label=0)}")

適合率の算出に使用する分母は陽性と予測したサンプル数であり、偽陽性件数を減らすことが適合率の向上につながります。

また混同行列の上部合計に対して、正解がどのくらいだったを示しています。

[実行結果]

テストデータの適合率は87.93%となっています。

前回記事の混同行列を見ると真陽性（左上）の５１件と、偽陽性（右上）の７件を足すと５８件となりこれが分母となります。

５８件のうち正しく予測できた５１件を分子として計算すると、今回のテストデータ適合率0.879と一致します。

再現率

再現率は、モデルがどれだけ網羅的に予測できているかを示す指標です。

再現率の算出には、recall_scoreを使用します。

[Google Colaboratory]

1
2
3
4
from sklearn.metrics import recall_score

print(f"訓練データ再現率：{recall_score(y_train,y_train_pred,pos_label=0)}")
print(f"テストデータ再現率：{recall_score(y_test,y_test_pred,pos_label=0)}")

再現率の算出に使用する分母は実際に陽性であるサンプル数であり、偽陽性件数は考慮されません。

偽陽性が増えても多くの悪性を検出したい場合は、再現性を重視した方がよいことになります。

また混同行列の左部合計に対して、正解がどのくらいだったを示しています。

[実行結果]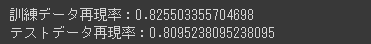

混同行列を見ると真陽性（左上）の５１件と、偽陰性（左下）の１２件を足すと６３件となりこれが分母となります。

６３件のうち正しく予測できた５１件を分子として計算すると、今回のテストデータ再現率0.809と一致します。

再現率(80.9%)は適合率(87.9%)と比較して低い結果となっています。

F1値

F1値は適合率と再現率 両方のバランスを考慮した指標です。

適合率と再現率の調和平均をとったものがF1値となります。

F1値の算出には、f1_scoreを使用します。

[Google Colaboratory]

1
2
3
4
from sklearn.metrics import f1_score

print(f"訓練データF1値：{f1_score(y_train,y_train_pred,pos_label=0)}")
print(f"テストデータF1値：{f1_score(y_test,y_test_pred,pos_label=0)}")

[実行結果]

適合率と再現率の間をとったような結果(84.29%)になりました。

F1値は、分類モデルの総合的な評価指標として使用されることが多いです。

ただし運用で使えるモデルかどうかを測るためには、F1値だけではなく、適合率や再現率などの個別指標にも注意する必要があります。